It is not necessary for the trapezoid to be isosceles. Take any trapezoid ABCD with diagoinals AC and BD intersecting at E. Let a = AB and b = CD. Let c be the length of the segment FG parallel to the two bases of the trapezoid. Our problem is to express c in terms of a and b.

---------------------------------

Extend sides DA and CB to meet at H. Construct A line parallel to side DA through G and extend to where in meets AB in point J (external to AB) and CD in K (internal to CD).

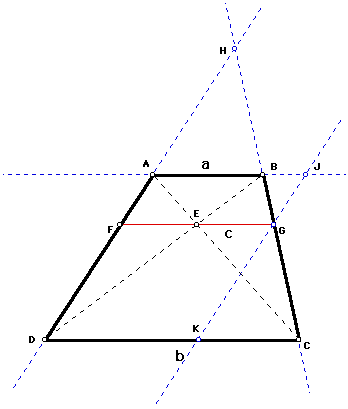
This produces the following similar triangles: HAB, HDC, GJB, GKC. Observe that in terms of a, b, and c, BJ = c - a and CK = b - c

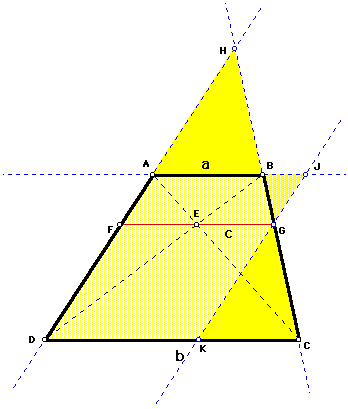
Therefore, considering triangles GJB and HAB, the ratio of similitude is and considering triangles GKC and HDC, the ratio of similitude is . Therefore we have a relation involving a, b, and c that we can solve for c.

 

If three numbers are such that by whatever part of itself the largest term exceeds the middle term, and the middle term exceeds the third by the same part of the third then the middle term is the harmonic mean of the first and third. This is the relationship shown in this equation. Usually the relation is written in one of the following forms to show that c is the harmonic mean of positive numbers a and b:

or

 

Thus the length of the parallel line segment through the intersection of the diagonals is the harmonic mean of the bases of the trapezoid.