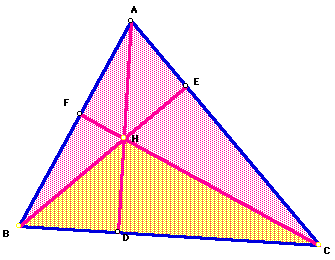

The ratio of the areas of triangles HBC and ABC is the same as the ratio HD/HD. Hence, considering all three cases,
But, the products, AD.BC, BE.AC, and CF.AD, are all the same, each being twice the area of the triangle ABC. Thus they could be written over a common denominator K = twice the area.

Interpret each of the three products. Each is twice the area of one of the three subtriangles with vertex at H and a base along once side of triangle ABC. There for the sum of these products is K and the result for the first equation is obtained.