

Given AC, CB, AD, DB such that AC + CB = AD + DB.
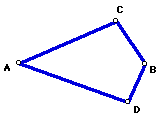
Extend AC and DG to intersect at point X.
Extend AD and CG to intersect at point Y.
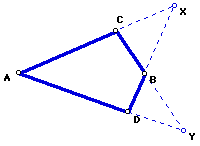
Prove that AX + XB = AY + YB.
Comment --
If we consider points A and B as the foci of an ellipse, then by the definition of an ellipse, that it is the locus of points with distances from two foci a constant sum, then points C and D are points on the ellipse.
Does this help? Is there any argument that points X and Y will be points on an ellipse with focal points A and B?