


Take any triangle and divide each side into three equal segments.
Connect each vertex to the first one-third point on the opposite side going around the triangle in the same direction. As follows:
What can be said about the triangle in the center formed by the three intersection points of the internal segments?

Similar? It easy to see with a GSP sketch that a counterexample can be generated. Click here for a GSP sketch. Drag one vertex to see how the shape of the small triangle varies as the shape of the large triangle changes.
It is, for example, easy to show a right triangle in the center when the large triangle clearly is not:

or a right triangle for the large triangle where the center triangle is clearly not a right triangle:
What about the ratio of the two areas?
1. Show that the center triangle has its area is one-seventh of the area of the original triangle.
Comment: If the connecting lines are drawn to the "2/3 point" rather than the "1/3 point" we should get the same ratio.
2. If both triangles are constructed, the overlap is a hexagon. What is the ratio of the area of this hexagon to the area of the original triangle?
3. Repeat the problem dividing each side into fourths.
4. Generalize to n sections on each side.
5. Repeat the construction with a triangle formed by lines and let the cut points be on the extensions of the sides:
Investigate . . .
Make a GSP sketch to animate the cut point along the three sides proportionally.
6. Develop a function for the ratio of the areas of the two triangles as the number of sections on each side increases. Plot the function.
7. (From Herb Bailey) Show that the two triangles have the same centroid
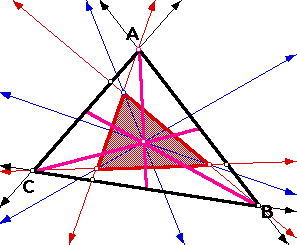
Here is a sketch with the medians of each triangle drawn.
Click here for an animated GSP sketch to investigate the centroids.
Reference:
Steinhaus, H. (1950) Mathematical Snapshots. Oxford: Oxford University Press.