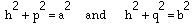Heron's Formula -- An algebraic proof

Jim Wilson

The demonstration and proof of Heron's formula can be done from elementary consideration of geometry and algebra.    This is the usual proof found in the literature and it is simple but tedious.  It has the limitation of never showing the role  s  in the formula except as a simplication at the end of the derivation.

I will assume the Pythagorean theorem and the area formula for a triangle

where b is the length of a base and h is the height to that base.

We have

so, for future reference,

2s = a + b + c
2(s - a) = - a + b + c
2(s - b) = a - b + c
2(s - c) = a + b - c

There is at least one side of our triangle for which the altitude lies "inside" the triangle. For convenience make that the side of length c. It will not make any difference, just simpler.

Let p + q = c as indicated. Then