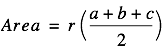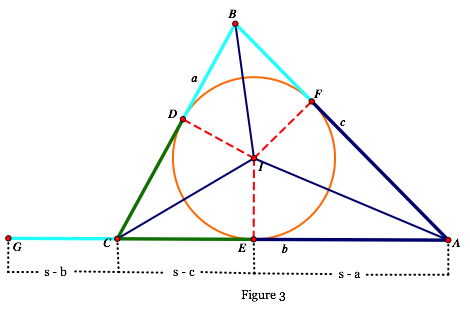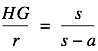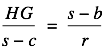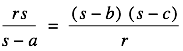An Elegant Geometric Derivation
Jim Wilson
Let us take a triangle ABC with sides of length a, b, and c. I will follow the convention of indicating the length a opposite the angle A and similarly for the other two pairs. Figure 1 is our triangle so labeled. If you want to skip the preliminary details of getting ready for the proof, move ahead to the discussion of Figure 4.
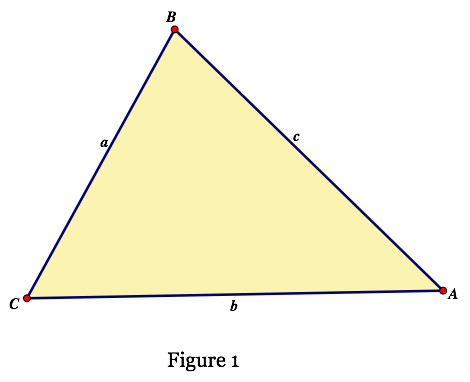
If we add the incircle to our construction and indicated the points of tangency with the sides there are several relationships that can be easily shown. If they are not immediately clear, they can be easily proven. See Figure 2.
We have added several things to our image. These include the incircle with center at I, the points of tangency of the incircle with the sides of the triangle at D, E, and F, line segments connecting I to each of the vertices, and radii of the incircle indicated by dashed lines.
Observe that if we have three triangles with a common vertex at I that cover the area of our original triangle. Thus, if we could express the length of the radius r of the incircle in terms of side lengths a, b, and c, we could derive a formula for the area of the original triangle in terms of the lengths of its three sides.
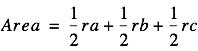
The expression in parentheses is the semiperimeter of the triangle s and so Area = rs.
The semiperimeter can be expressed as the sum of 3 segments, each half the length of a side. It is convenient to locate these segments in Figure 2. From each vertex, the distances to the points of tangency on the adjacent sides are equal. We have illustrated that with colors of the respective line segments from each vertex. We have AE = AF, BF = BD, and CD = CE. If we construct a segment CG along AC extended and let CG = BF, then the length AG is the semiperimeter.
Now the three segments along AG (length s) have lengths s – a, s – b, and s – c. We need something more, probably some similar triangles, in order to find some expression for the radius r in terms of s, a, b, and c.
We are now going to suppress some of the added line segments for a moment and and some others. In particular, the construction of point G seems rather arbitrary. It would be nice if it related to something. In Figure 4, we have added the excircle that is tangent to side BC of the triangle. This excircle is externally tangent to side AC and side AB. The distances from A to each of the external tangent points on sides AC and AB are equal and that distance is s. Thus G is a point of tangency of the excircle. The excenter is H and HG is a radius of the excircle.
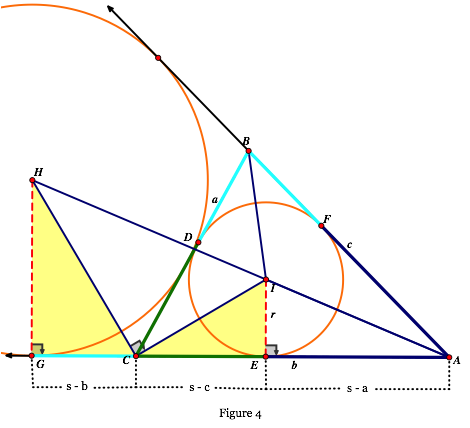
We now have two pairs of similar triangles HGA and IEA; HGC and CIE.
The first pair are similar because IE and HG are parallel. Therefore from the first pair we get
The second pair are similar. One way to show that the second pair are similar is to observe that HC and IC are exterior angle and interior angle bisectors from point C. Therefore they are perpendicular and thus the angles GCH and ICE are complementary. This leads to the congruence of angle GHC and ECI. The similarity gives
Now solve each for HG and set the two resulting expressions equal to give
Now,
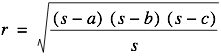
Since Area = rs we have
Recognize the intermediate derivation was to find an expression for the radius r of the incircle in terms of the lengths of the sides. This is the underlying strategies for some other proofs.
Return