
Given any triangle ABC and an arbitrary point M in its interior. Extend segments from each vertex through M to intersect the opposite sides, giving the segments AD, BE, and CF. Form the ratios of segments
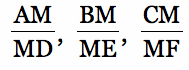
Exploration with GSP Measurements and constructions
The explorations leads to a strong conjecture that the expression of the product of the ratios minus the sum of the ratios is a constant. However, measurement is not proof. The problem is now to prove that the expression is a constant AND to determine what that constant value is.
One approach
The ratios in the expression we want to evaluate are of the parts of the three Cevians through M. If we could find similar triangles to allow substitutions appropriately, we might be able to write an equivalent expression in terms of the ratios along the sides. That could permit the use of Ceva's theorem where
The approach here will be to construct auxilliary lines so that similar triangles can be found that allow substitution for the three ratios.
In a similar manner, construct a line parallel to BE we can arrive at
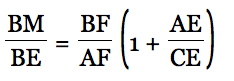
and a line parallel to CF to arrive at
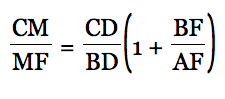
Finishing it.
It will simplify our notation if we let
These three ratios of segments on the sides of the triangle are constructed by the same orientation on each side. By Ceva's Theorem we know that
xyz = 1 Now, the difference of the product and the sum of the segments on the Cevians through M is
= [x(1 + z)y(1 + x)z(1 + y)] - [x(1 + z) + y(1 + x) + z(1 + y)]
= [xyz(1 + z)(1 + x)(1 + y) ] - [x + y + z + xy + yz + xz]
= [xyz(1 + x + y + z + xy + yz + xz + xyz) ] - [x + y + z + xy + yz + xz]
= [2 + x + y + z + xy + yz + xz ] - [x + y + z + xy + yz + xz]
= 2 +[x + y + z + xy + yz + xz ] - [x + y + z + xy + yz + xz]
= 2