
The Conics
By: Diana Brown
Day Eight:
Hyperbola Introduction
How to Construct A Hyperbola Using Wax Paper:
Start out with a piece of uncrumbled wax paper about the size of
half a sheet of standard notebook paper (8.5 x 11). Draw a circle in the center
of the wax paper without writing off the paper. Then draw a point
anywhere outside the circle excluding on the circle. The next step
is to fold up the point onto the circle so they are touching. When this
point is aligned onto the circle, crease the paper and fold it
accordingly. Choose another part of the circle and align this with the
point, creasing the wax paper. Repeat this step several times until the
point has touched the majority of the circle or until a hyperbola is visible.
How to Construct A Hyperbola Using Geometerís Sketchpad:
On
a new sketch, construct a circle with center A using the circle tool.†† Using the point tool, draw a point B outside
the circle (but not on it).

Select the point B and make a line segment between it and a point C on the
circle.
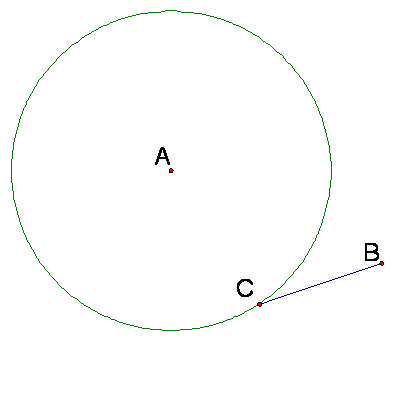
Place a point D at the midpoint of that segment.† Construct the perpendicular bisector of line
segment BC and while this line is still selected, choose Trace Line from the
Display menu.
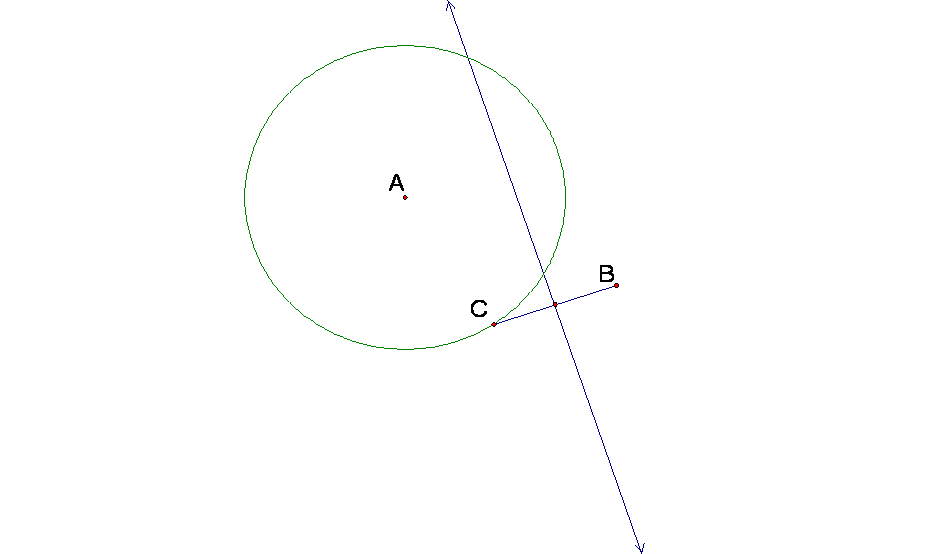
Highlight
point C and click animate point from the Display menu and watch the hyperbola
form!

Proof
Statement: The difference
of the distances from two points (the foci) inside a hyperbola to any point on
the hyperbola is constant.
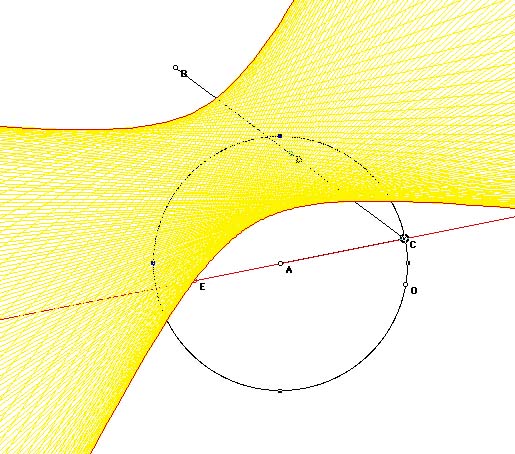
Proof: The foci on our sketch are again the points A (the center of the
circle) and B (the point outside the circle). We will again use
Geometer's Sketchpad to visualize our proof. Construct a line through
points A and C and place a point of intersection E where this new line
intersects the perpendicular line passing through point D. This point E
traces out the hyperbola. Construct a line segment between points E and
B. You should now have a triangle BCE with a perpendicular bisector
ED. Because ED is the perpendicular bisector, BD is congruent to DC and
the angles BDE and CDE are both 90 degrees. Of course, DE is congruent to
itself, and thus we have two triangles with two congruent sides with an
included congruent angle. By SAS, the triangles are congruent and
therefore EB is congruent to EC. The radius of the circle is AC and AE =
AC+EC. Then AE-EC = AC and therefore AE-BE=AC. So since the radius
is constant, the difference AE-BE is always constant.
Return to the Conics Homepage
Return to EMAT 6690 Homepage
Go to Day
Nine (Hyperbolas)