Assignment 9 continued:
Pedal Triangles & the Simson Line
by Kristina Dunbar, UGA
This page contains pedal triangles for special cases when the pedal point is on a side of the original triangle or at a vertex. We also discuss Simson Lines.
![]()
What happens when the pedal point P is on a side of triangle ABC?
Here's what it looks like:
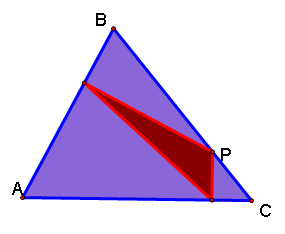
The above case is for an acute triangle. When the triangle is obtuse, it looks like this:
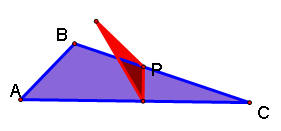
When the original triangle is right, the pedal triangle looks like the one below:
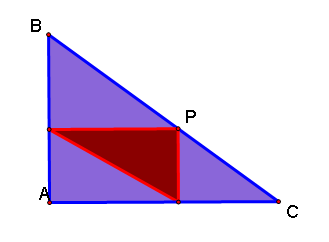
The pedal triangle is also a right angle!
Click here for a GSP construction of the above cases.
![]()
What happens when the pedal point P is on a vertex of triangle ABC?
Here's what it looks like:
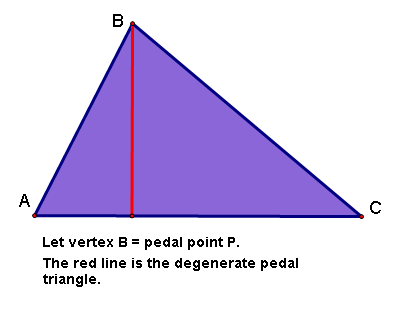
When the pedal point P is on a vertex of the original triangle, all of the vertices of the pedal triangle are collinear.
![]()
A Simson Line is when all three vertices of the pedal triangle are collinear, forming a degenerate triangle.
When the pedal point is on a vertex of the original triangle, it does not matter what shape the original triangle is, the pedal triangle will always form the Simson Line. In the case where P is on a vertex, the Simson Line will always be an altitude of the original triangle. However, there are other cases in which the pedal triangle is a Simson Line, and it does not always have to be an altitude.
![]()
Return to my Home Page.
Return to Pedal Triangles Page 1, Page 2, or Page 3.
Return to TOP.
Continue Exploring Pedal Triangles.
![]()