
Parametric
Equations for a Cycloid
by
Gayle Gilbert & Greg Schmidt
Let ![]() be a point on a circle of radius
be a point on a circle of radius ![]()
Consider the curve, which is traced out by the point as the
circle rolls along the ![]() -axis. We will
allow that our circle begins to trace the curve with the point
-axis. We will
allow that our circle begins to trace the curve with the point ![]() at the
origin.
at the
origin.
Click here to see the animation in GSP.
Such a curve is called a cycloid.
Now, we can find the parametric equation fir the cycloid as follows:
Let the parameter be the angle of rotation of ![]() for our given
circle. Note that
for our given
circle. Note that ![]() when the point
when the point ![]() is at the
origin.
is at the
origin.
Next consider the distance the circle has rolled from the
origin after it has rotated through ![]() radians, which
is given by
radians, which
is given by
![]()
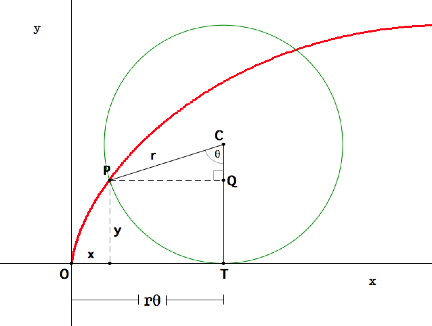
And so we can see that the center of the circle is given by ![]()
![]() .
.
Now, letting the coordinates of P be ![]() we have
that
we have
that
![]()
and
![]()
Hence, we have
![]() ,
,
![]()
![]()
which gives us the parametric equations of the cycloid.