INTRODUCTION:
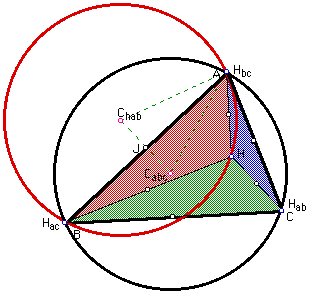
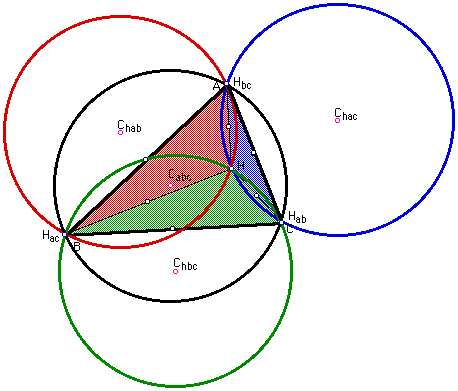
In this write-up we will take a look at a triangle ABC. First we will find the orthocenter, H, of this triangle. Then we will construct the triangles, HBC, HAB, and HAC along with their circumcenters and circumcircles. We will also construct the circumcenter and circumcircle for triangle ABC. The diagram of these constructions is pictured below. After constructing this it appears that the four circumcircles are all the same size. By same size, I mean that they appear to have the same area. Therefore, the hope of this write up is to prove this conjecture.

Before we being the proof we can use GSP to give us a measurement of the circles to give us an indication of whether or not the conjecture is true. Here are the results:
GREEN-Area(Circle
C(hbc)H(ab)) = 53.258 square cm
BLACK-Area(Circle C(abc)H(ab)) = 53.258 square cm
BLUE-Area(Circle
C(hac)H(bc)) = 53.258 square cm
RED-Area(Circle
C(hab)H(ac)) = 53.258 square cm
PROOF:
To prove our conjecture it is sufficient to prove that the area of the black circle is equal to the area of any of the other three circles. Let us choose the red circle and prove that it's area is equal to the area of the black circle. It should be clear that the area of the green and blue circles could be proven equal in a similar fashion.