Paraboloids (3 dimensional parabolas) are all around us in every day life. Satelite dishes, automobile headlights, telescope lenses, and even our own outdoor amphitheater are some examples of objects that are parabolic in nature. If we took a cross section of any of these objects, we would have a parabola.

The previous nine units dealt with the algebra of parabolas. This final unit will reveal a very different perspective on parabolas. The construction below was done with GSP 4.01. Other versions of GSP may not have the same menu features. Open your own GSP sketch and construct your own parabola as you follow along.

A geometric definition of a parabola is the locus of points that are equidistant from a fixed point called the focus, and a fixed line called the directrix. We can use Geometer's Sketchpad to illustrate this definition. To do so, we first need to draw our focus and directrix as shown.

We can do this by choosing the line tool from the tool bar. Click in the GSP window and drag the mouse to make a line (the directrix) somewhere toward the bottom of your window. Next choose the point tool and put a point in the window ( for convenience sake, put the point about an inch or two above the directrix). Next, put another point on the directrix. Label this point B and select points A and B and connect them using the segment command under the "Construct" menu. Now use the Midpoint command under the "Construct" menu to construct the midpoint of segment AB. Label this point M.

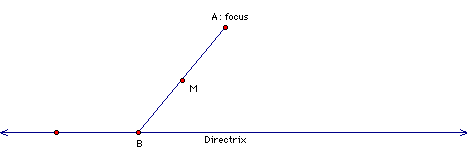
Now we will construct a line perpendicular to M (label it T for reasons we will get to later), and a line perpendicular to the Directrix through point B. Select these two lines and "Construct" the point at their intersection. Label the intersection point P.

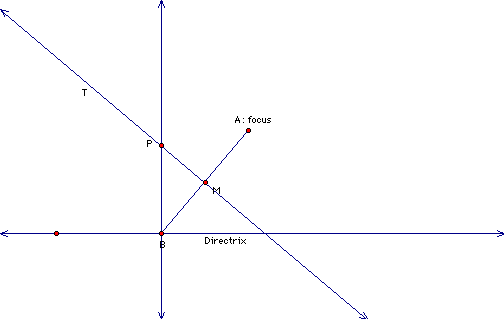
Take a break for a moment and play with your sketch. Use the arrow tool and move point B along the directrix. Make some conjecture about the path of point P. Goto the edit menu. Choose Preferences...color, then put a check in the box labeled "fade traces over time". Select point P. Goto the Display menu and choose Trace Intersection. Now go back and play with your sketch again. Were you right about the path of point P?

The remainder of the sketch is simply cleaning things up so that we can better understand why the locus of points that point P traces out is a parabola by definition. Select points P, B, and A and choose "Construct" segments. Now select the line through PB perpendiclar to the directrix. Goto the Display menu and choose Hide Perpendicular Line. Now, select segments BP and AP. Goto the Calculate menu and select length. Play with your graph some more by moving point B along the directrix. Also move the focus around and see what effecth this has on your traces.

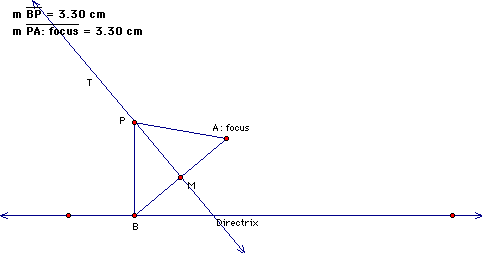
Finally, we can animate our sketch so that we do not have to move B manually. To do this, select point B. Goto the Edit menu and choose Action Buttons-Animation. You want to animate point B bidirectionally along line directrix. A button will appear that says Animate Point. Knock yourself out. You can stop the animation by clicking on this button again. Here is the complete construction if you are unable to get it working yourself.

For those of you with a Geometry background, write a proof that explains why this construction works (hint: you must prove two triangles congruent).

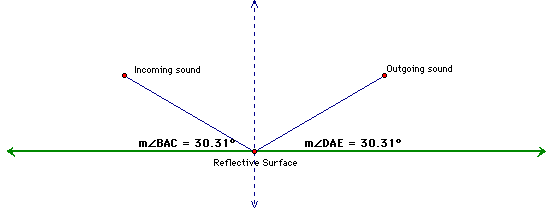
Parabolas and paraboloids are particularly useful in the real world because of their reflective properties. Think of the example of a sound dish like the ones you see on the sidelines of a pro football game. The person using the dish will point it in the direction of the sound that he/she wishes to "collect". In physics class, we learn that the angle of incidence is equal to the angle of reflection. In other words, the sound will bounce off of a flat surface at the same angel it comes into it as illustrated below

In a parabola, we must imagine the sound reflecting off of a line tangent to the parabola at a given point. We will first look at a trace of some lines tangent to the parabola.

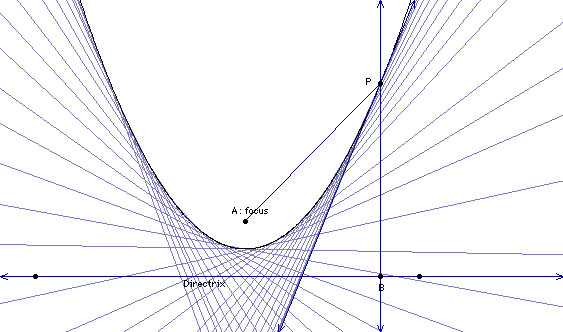
Now let's illustrate what happens to the sound as it enters the paraboloid perpendicular to the directrix. Make some conjecture as to what happens to the sound in our dish. Why do you suppose the fixed point in the geometric definition of a parabola is called the focus?

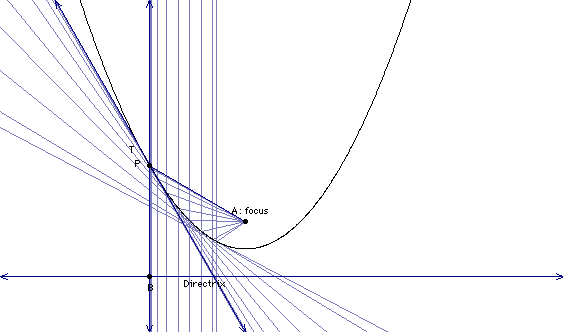
There is much more to be discussed and discovered here. For example. If we wanted to design a sound collection dish like the one above, how would we figure out where to put the focus? In other words, how far from the vertex of the dish should the sound collection device be placed. What if we were designing a car headlight. The paraboloid in the headlight is used to reflect the beam of light in a particular direction. How is this achieved? Where does the light have to be placed to maximize night vision while driving? As your final task, choose one of the real world applications of paraboloids above or find another use of paraboloids in the real world. Explain how your paraboloid functions and write several questions that you would have to answer if you were designing the object chosen.