
| This is the write-up of the Final Assignment |
Brian R. Lawler
|
| EMAT 6680 |
12/16/00
|
| C. |
Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4? |
| When P is placed at the centroid G, the result is four congruent triangles. Hence, the area of triangle DEF is 1/4 the area of triangle ABC. | 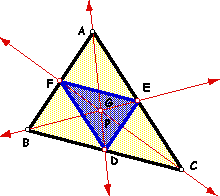 |
 |
Comments? Questions? e-mail me at blawler@coe.uga.edu |
| Last revised: January 3, 2001 |
|