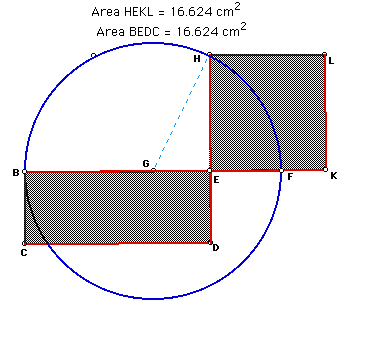
To prove this claim, let a, b, and c be the lengths of HG, EG and EH, respectively.

Given triangle GEH is a right triangle, then by using the pythagorian theorem gives us or It can be noted that length FG = BG = HG = a since all are radii of the circle as shown above.Therefore length EF = FG - EG = a - b and length BE = BG + GE = a + b. It follows that

area of rectangle BCDE = (base)*(height).

area of rectangle BCDE = (BE)*(ED)

area of rectangle BCDE = (BE)*(EF) given length EF = ED

area of rectange BCDE = (a + b)(a - b) as noted above

area of rectange BCDE =

area of rectangle BCDE == area of square HEKL as shown above.

Back to quadrature of rectange page