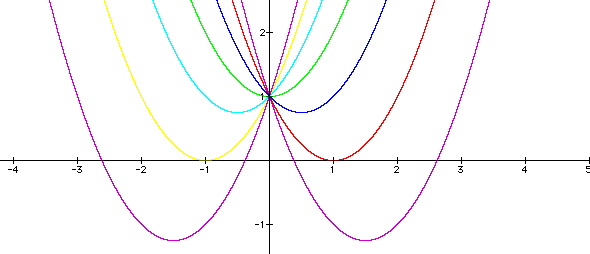
Now consider the graph below
of for b = -3, -2,
-1, 0, 1, 2, 3, note the "movement" of a parabola as
the value of b is changed. Also, all parabolas of this type passes
through the same point on the y-axis i.e(0,1). For more illustration
click Graphing Calc
#3. For b = -2, the
parabola is tangent to the X- axis hence, one real root at the
point of tangency. For -2<b<2, the parabola does not intersect
the X= axis, therefore, no real roots. Similarly for b=2, the
parabola is tangent to the x-axis (one real negative root) and
for b>2, the parabola intersects the x-axis twice hence two
real roots.
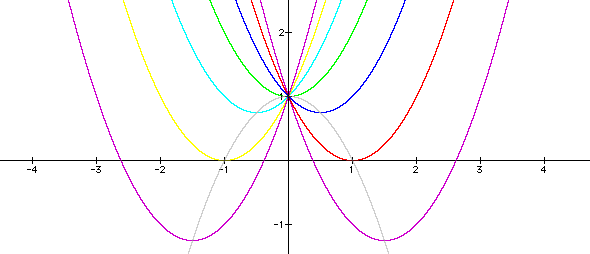
Examining the locus of vertices of the parabolas
as b varies is also instructive in this situation. This time the
locus of vertices forms a parabola, whose equation is
,
as you can see by viewing the grey graph below.
To prove that is
the locus of the vertices of the parabola, consider the set of
vertices of all
quadratics of the form 
By rewriting in vertex form
,
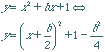
the general form of the vertices can be
seen to be 
.
Substituting 3 values for b will
identify 3 particular points. The
unique quadratic through those three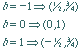 
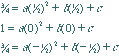
points can identified with linear
algebra.
Hence,
passes
through all vertices.
Back to Samuel's page