

In this write-up, I investigate the quadratic equation y = ax2 + bx + c and analyze what happens to the graph of the equation as two values are fixed and one value varies. I note that the characteristics of a parabola are its x-intercepts, y-intercept, axis of symmetry, vertex, and whether it opens up or down. Therefore, first I fix the values of "b" and "c" at 1 and examine what happens to the graph as I vary the values of "a". Then, I fix the values of "a" and "c" at 1 and examine what happens to the graph as I vary the values of "b". Finally, I fix the values of "a" and "b" at 1 and examine what happens to the graph as I vary the values of "c".
In this section, I examine the effects on varying the values of "a" using the equation y = ax2+ x + 1 (notice the values of "b" and "c" are fixed at one).
1) This graph was created using "a" values of -4 (red), -2 (green), 0 (turquoise), 2 (blue), and 4 (purple).
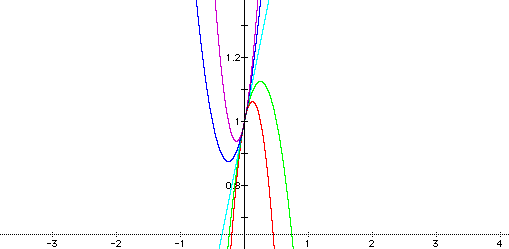
2) This graph was created using "a" values of -9 (red), -7(green), -5 (turquoise), -3 (blue), and -1 (purple).
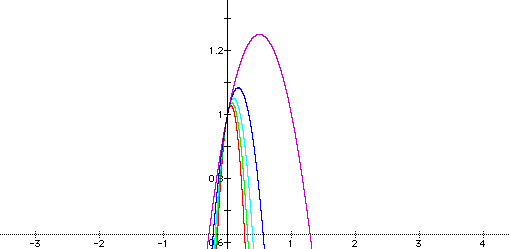
3) This graph was created using "a" values of 1 (red), 3 (green), 5 (turquoise), 7 (blue), and 9 (purple).
To see a QuickTime movie of y = ax2 + x + 1 as the values of "a" vary from -10 to 10 and back, click here.
Based on the example graphs, it seems obvious that the value of "a" has some effect on the x-intercepts of the graph. I can check this by completing the square on the equation ax2 + x + 1 = 0. First, I divide by "a," so x2 + x/a + 1/a = 0. Therefore, x2 + x/a + 1/4a2 = -1/a + 1/4a2. Factoring on the left gives (x + 1/2a)2 = (-4a + 1)/4a2. Taking the square root of each side leaves x + 1/2a = +/- sqrt(1 - 4a)/2a. Finally, x = (-1 +/- sqrt(1 - 4a))/2a. Since the variable "a" is left in the equation, I know that its value affects the location of the x-intercepts.
It is also easy to notice that the y-intercept of each graph remains constant. Therefore, I can assume that the value of "a" does not affect the y-intercept of the graph. This should make sense, because to find the y-intercept of a graph, we let x = 0. If x = 0 in the above situation, then the equation y = ax2 + x + 1 reduces to y = 1. Therefore, the x2 term has disappeared, and so the value of "a" has no bearing on the y-intercept.
I conjecture that the value of "a" does have effects on the axis of symmetry. The equation of the axis of symmetry is found by averaging the x-coordinates of the x-intercepts. Therefore, [((-1 + sqrt(1 - 4a))/2a) + ((-1 - sqrt(1 - 4a))/2a)]/2 = (-2/2a)/2 = (-1/a)/2 = -1/2a. So the equation of the axis of symmetry is x = -1/2a. Thus, the value of "a" affects the location of the axis of symmetry. Furthermore, if "a" is positive, the equation of the axis of symmetry is negative, and so the axis of symmetry (and vertex) will be to the left of the y-axis. If "a" is negative, the equation of the axis of symmetry is positive, and so the axis of symmetry (and vertex) will be to the right of the y-axis. Note that when a = 0, the axis of symmetry is undefined (the equation actually becomes linear, so the graph is a line in this case).
Since the vertex of the parabola is on the axis of symmetry, it follows that the vertex must be affected by the value of "a." The x-coordinate of the axis of symmetry is -1/2a, and the y-coordinate can be found by substituting this value into the equation y = ax2 + x + 1. By doing so, y = a(-1/2a)2 + (-1/2a) + 1 = a(1/4a2) - 1/2a + 1 = 1/4a - 2/4a + 4a/4a = (4a - 1)/4a.
Finally, when "a" is positive, the parabola opens up and has a minimum. When "a" is negative, the parabola opens down and has a maximum.
In this section, I examine the effects on varying the values of "b" using the equation y = x2+ bx + 1 (notice the values of "a" and "c" are fixed at one).
1) This graph was created using "b" values of -4 (red), -2 (green), 0 (turquoise), 2 (blue), and 4 (purple).
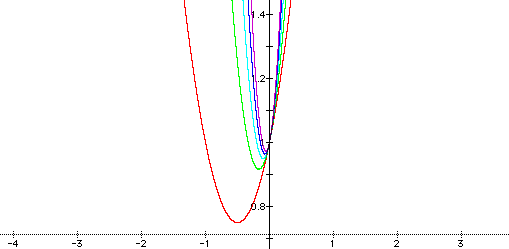
2) This graph was created using "b" values of -5 (red), -4(green), -3 (turquoise), -2 (blue), and -1 (purple).
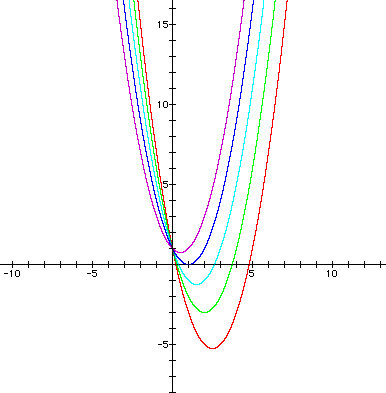
3) This graph was created using "b" values of 1 (red), 2 (green), 3 (turquoise), 4 (blue), and 5 (purple).
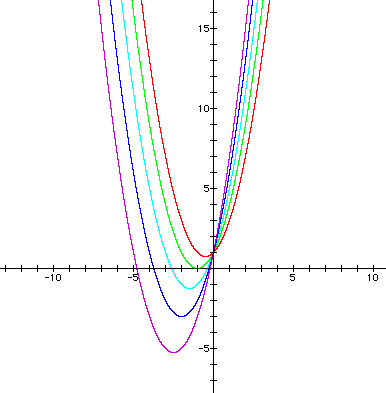
To see a QuickTime movie of y = x2 + bx + 1 as the values of "b" vary from -10 to 10 and back, click here.
Based on the example graphs, it seems obvious that the value of "b" has some effect on the x-intercepts of the graph. I can check this by completing the square on the equation x2 + bx + 1 = 0. First, x2 + bx + b2/4 = -1 + b2/4. Factoring on the left gives (x + b/2)2 = (-4 + b2)/4. Taking the square root of each side leaves x + b/2 = +/- sqrt(b2 - 4)/2. Finally, x = (-b +/- sqrt(b2 - 4))/2. Since the variable "b" is left in the equation, I know that its value affects the location of the x-intercepts.
Again, it is easy to notice that the y-intercepts of each graph remain constant. Therefore, the value of "b" does not affect the y-intercept of the graph. This should make sense, because to find the y-intercept of a graph, we let x = 0. If x = 0 in the above situation, then the equation y = x2 + bx + 1 reduces to y = 1. Therefore, the x term has disappeared, and so the value of "b" has no bearing on the y-intercept.
I conjecture that the value of "b" does have effects on the axis of symmetry. The equation of the axis of symmetry is found by averaging the x-coordinates of the x-intercepts. Therefore, [((-b + sqrt(b2 - 4))/2) + ((-b - sqrt(b2 - 4))/2)]/2 = (-2b/2)/2 = -b/2. So the equation of the axis of symmetry is x = -b/2. Thus, the value of "b" affects the location of the axis of symmetry. Furthermore, if "b" is positive, the equation of the axis of symmetry is negative, and so the axis of symmetry (and vertex) will be to the left of the y-axis. If "b" is negative, the equation of the axis of symmetry is positive, and so the axis of symmetry (and vertex) will be to the right of the y-axis.
Since the vertex of the parabola is on the axis of symmetry, it follows that the vertex must be affected by the value of "a." The x-coordinate of the axis of symmetry is -b/2, and the y-coordinate can be found by substituting this value into the equation y = x2 + bx + 1. By doing so, y = (-b/2)2 + b(-b/2) + 1 = b2/4 - b2/2 + 1 = b2/4 - 2b2/4 + 4/4 = (-b2 + 4)/4.
Finally, the value of "b" seems to have no bearing on whether the parabola opens up or down.
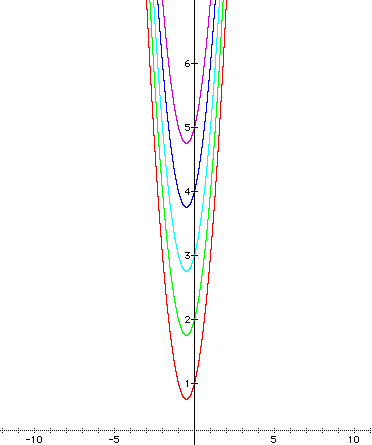
In this section, I examine the effects on varying the values of "c" using the equation y = x2+ x + c (notice the values of "a" and "b" are fixed at one).
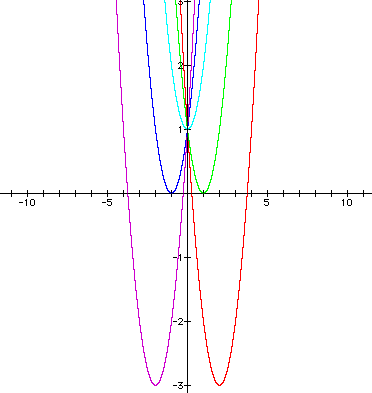
1) This graph was created using "c" values of -2 (red), -1 (green), 0 (turquoise), 1 (blue), and 2 (purple).
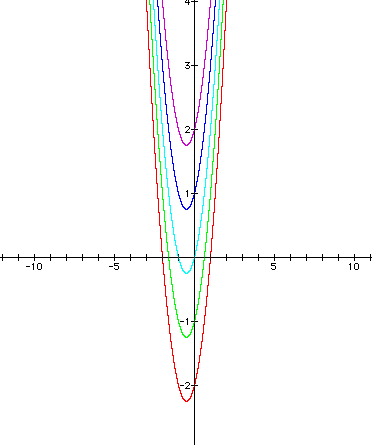
2) This graph was created using "c" values of -5 (red), -4(green), -3 (turquoise), -2 (blue), and -1 (purple).
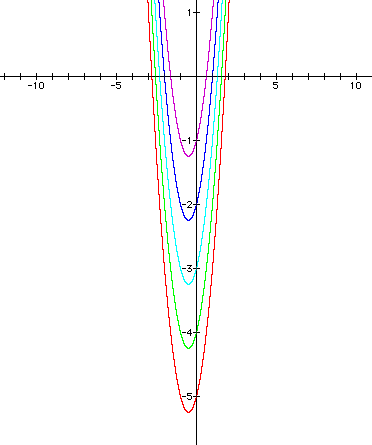
3) This graph was created using "c" values of 1 (red), 2 (green), 3 (turquoise), 4 (blue), and 5 (purple).
To see a QuickTime movie of y = x2 + x + c as the values of "c" vary from -10 to 10 and back, click here.
Based on the example graphs, it seems obvious that the value of "c" has some effect on the x-intercepts of the graph. I can check this by completing the square on the equation x2 + x + c = 0. First, x2 + x + 1/4 = -c + 1/4. Factoring on the left gives (x + 1/2)2 = (-4c + 1)/4. Taking the square root of each side leaves x + 1/2 = +/- sqrt(1 - 4c)/2. Finally, x = (-1 +/- sqrt(1 - 4c))/2. Since the variable "c" is left in the equation, I know that its value affects the location of the x-intercepts.
Obviously, the value of "c" affects the y-intercept of the graph. This should make sense, because to find the y-intercept of a graph, we let x = 0. If x = 0 in the above situation, then the equation y = x2 + x + c reduces to y = c. Therefore, the value of "c" is the y-intercept of the graph.
I conjecture that the value of "c" does not have effects on the axis of symmetry. The equation of the axis of symmetry is found by averaging the x-coordinates of the x-intercepts. Therefore, [((-1 + sqrt(1 - 4c))/2) + ((-1 - sqrt(1 - 4c))/2)]/2 = (-2/2)/2 = -1/2. So the equation of the axis of symmetry is x = -1/2. Thus, the value of "c" has no effect on the location of the axis of symmetry.
But I do submit that the vertex must is affected by the value of "c." The x-coordinate of the axis of symmetry is -1/2, and the y-coordinate can be found by substituting this value into the equation y = x2 + x + c. By doing so, y = (-1/2)2 + (-1/2) + c = 1/4 - 1/2 + c = 1/4 - 2/4 + 4c/4 = (4c - 1)/4.
Finally, the value of "c" seems to have no bearing on whether the parabola opens up or down.