

In this write-up, I investigate the Simson Line of a triangle. I start with a quick description of the pedal triangle and then move on to the definition and construction of the Simson Line. Next, I find the envelope of the Simson Line, followed by a conjecture of the special positions of the pedal point, P, that make the Simson Line one of the sides of the original triangle. Then, I construct the orthocenter, H, of the original triangle, the segment HP, and conjecture about the intersection of the segment HP and the Simson Line. Finally, I construct two pedal points on the same circumcircle and their Simson Lines, and then I conjecture about the relationship between the angle of intersection of the two Simson Lines and the angular measure of the arc between the two pedal points.
To form a pedal triangle, start with any triangle ABC and any point P in the plane. Extend sides AB, AC, and BC to be lines. Construct the perpendiculars from point P to each extended side of the triangle, and construct the three points of intersection. Then construct the segments that connect these three points of intersection; this triangle is called the pedal triangle, and point P is called the pedal point.
In the diagram below, triangle ABC is the given triangle, point P is the pedal point, and triangle RST is the pedal triangle.
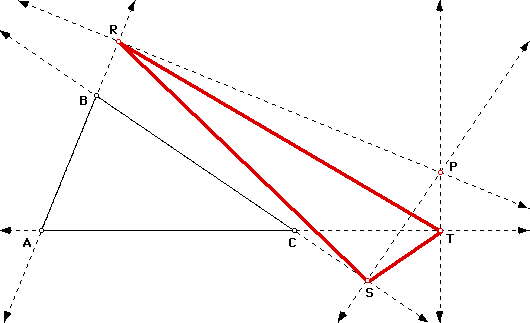
Note that point P can be any point in the plane. Therefore, as P moves around the plane, the pedal triangle RST changes size, shape, and location.
Click here to download a GSP file of a pedal triangle to manipulate.
Click here to download a GSP script to make a pedal triangle of your own.
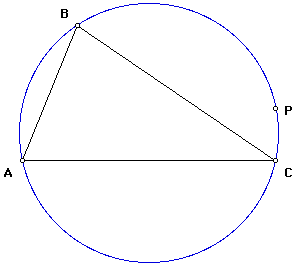
Something very interesting happens when the pedal point P is chosen to be a point on the circumcircle of triangle ABC.
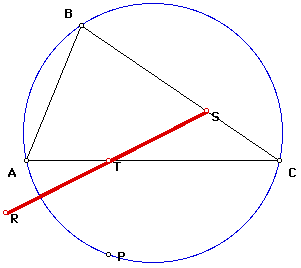
This choice of location for the pedal point P causes the vertices of the pedal triangle to be collinear. We can then say that the pedal triangle is degenerate; in other words, the pedal "triangle" has become a segment. This line segment is called the Simson Line.
Click here to download a GSP file of a Simson Line to manipulate.
Click here for a proof of the Simson Line.
If the Simson Line is extended from a segment to a line, the trace of the line as the pedal point P moves around the circumcircle can be found.
The following diagram shows the envelope of the Simson Line. The "lighter" red is the trace of the extended line, and the "darker" red actually shows the locus of the Simson Line segment itself.

Click here to download a GSP file of the trace of a Simson Line.
There are special points on the circumcircle for the pedal point P such that the Simson Line becomes one of the sides of the original triangle. Each situation occurs when P is one endpoint of a diameter of the circle and one of the vertices of the original triangle is the other endpoint.
In the following diagram, for the pedal triangle to become side AB of the original triangle, then the chord PC must be a diameter of the circle.
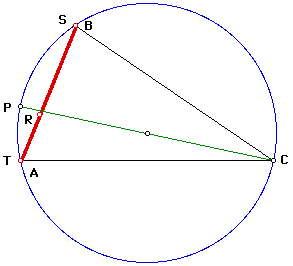
In the following diagram, for the pedal triangle to become side BC of the original triangle, then the chord PA must be a diameter of the circle.
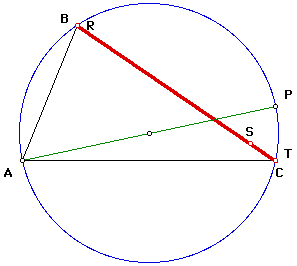
In the following diagram, for the pedal triangle to become side AC of the original triangle, then the chord PB must be a diameter of the circle.
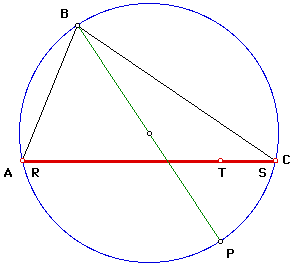
Click here to download a GSP file of the Simson Line and the chords PA, PB, and PC.
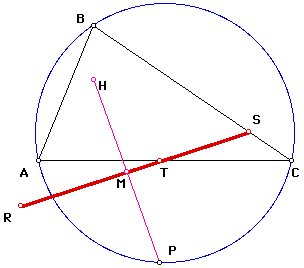
When the orthocenter, H, of the original triangle is found, and the segment HP is drawn, a unique relationship exists between this segment and the Simson Line.
In the following diagram, M is the point of intersection of the segment HP and the Simson Line.
It can be conjectured that the segments HM and MP are equal; in other words, M is the midpoint of HP.
Click here to download a GSP file of the Simson Line, the orthocenter H, and segment HP.
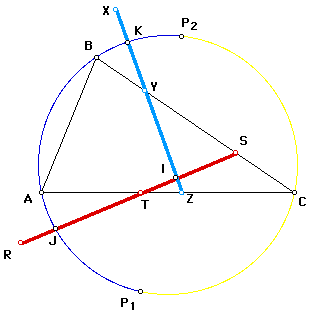
When two pedal points are chosen to be on the same circumcircle, and their respective Simson Lines are constructed, a unique relationship exists between the angle of intersection of the Simson Lines and the angular measure of the arc between the two pedal points.
In the following diagram, pedal point P1 creates the Simson Line containing the points R, S, and T (in red), and the intersection of this line and the circumcircle is point J. The pedal point P2 creates the Simson Line containing the points X, Y, and Z (in light blue), and the intersection of this line and the circumcircle is point K. The intersection of the two Simson Lines is point I, and the measured arc between P1 and P2 is in yellow.
It can be conjectured that angle JIK = 1/2 of the angular measure of the yellow arc between P1 and P2.
Click here to download a GSP file of two pedal points and their Simson Lines.