

There are many different types of mean in mathematics, all having different equations that can be used to find them. While most people can memorize these equations and the relationships among the types of mean, most never make the connection to geometry. In this essay, I present seven different types of mean and show how to construct them in a trapezoid. Then I compare their values by constructing all seven types of mean in one trapezoid.
Resource:
Eves, Howard (1992). An Introduction to the History of Mathematics. Saunders College Publishing: Philadelphia, Pennsylvania.
The arithmetic mean, "A," of any two real numbers "a" and "b" can be found using the following equation: A = (a + b)/ 2.
In a trapezoid with bases of lengths "a" and "b," the arithmetic mean, "A," is the length of the segment that is parallel to the bases and that also bisects the sides of the trapezoid.
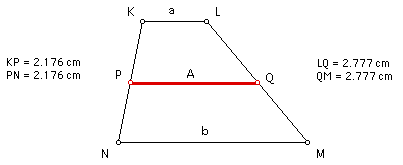
Click HERE to see a step-by-step construction of the arithmetic mean in a trapezoid.
The geometric mean, "G," of any two real numbers "a" and "b" can be found using the following equation: G = sqrt(ab).
In a trapezoid with bases of lengths "a" and "b," the geometric mean, "G," is the length of the segment that is parallel to the bases and that also divides the trapezoid into two similar trapezoids.
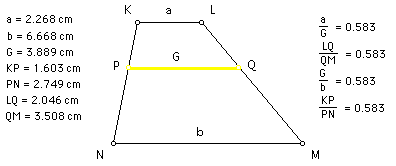
Click HERE to see a step-by-step construction of the geometric mean in a trapezoid.
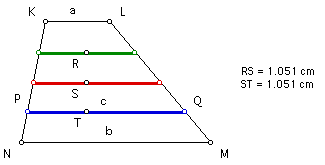
The harmonic mean, "H," of any two real numbers "a" and "b" can be found using the following equation: H = 2ab/(a + b).
In a trapezoid with bases of lengths "a" and "b," the harmonic mean, "H," is the length of the segment that is parallel to the bases and that also passes through the intersection of the diagonals of the trapezoid.
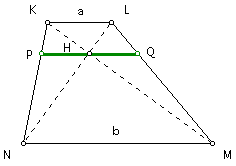
Click HERE to see a step-by-step construction of the harmonic mean in a trapezoid.
The heronian mean, "h," of any two real numbers "a" and "b" can be found using the following equation: h = (a + sqrt(ab) + b)/ 3.
In a trapezoid with bases of lengths "a" and "b," the heronian mean, "h," is the length of the segment that is parallel to the bases and that also is 1/ 3 the way from the arithmetic mean to the geometric mean.
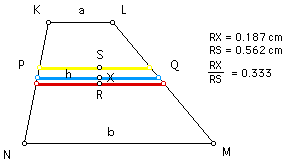
Click HERE to see a step-by-step construction of the heronian mean in a trapezoid.
The contraharmonic mean, "c," of any two real numbers "a" and "b" can be found using the following equation: c = (a^2 + b^2)/(a + b).
In a trapezoid with bases of lengths "a" and "b," the contraharmoic mean, "c," is the length of the segment that is parallel to the bases and that also is as far below the arithmetic mean as the harmonic mean is above the arithmetic mean.
Click HERE to see a step-by-step construction of the contraharmonic mean in a trapezoid.
The root-mean-square, "r," of any two real numbers "a" and "b" can be found using the following equation: r = sqrt((a^2 + b^2)/ 2).
In a trapezoid with bases of lengths "a" and "b," the root-mean-square, "r," is the length of the segment that is parallel to the bases and that also bisects the area of the trapezoid.
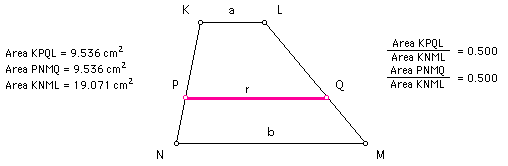
Click HERE to see a step-by-step construction of the root-mean-square in a trapezoid.
The centroidal mean, "g," of any two real numbers "a" and "b" can be found using the following equation: g = 2(a^2 + ab + b^2)/ 3(a + b).
In a trapezoid with bases of lengths "a" and "b," the centroidal mean, "g," is the length of the segment that is parallel to the bases and that also passes through the centroid of area of the trapezoid.
Click HERE to see a step-by-step construction of the centroidal mean in a trapezoid.
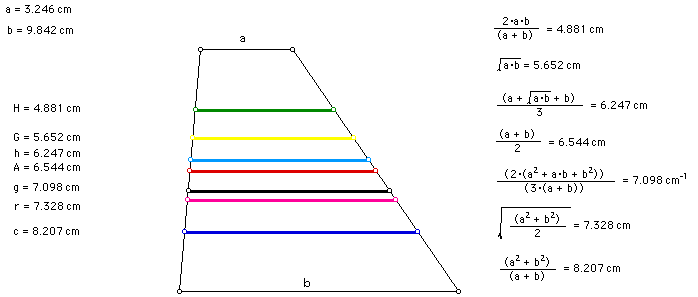
The seven types of mean presented above have the following relationships, when "a" and "b" are real numbers, and when "a" does not equal "b" :
Here is an example of a trapezoid that contains all seven of the means. The figure and measurements seem to support the above relationships.
Click HERE to see a proof that the above relationship is true.
So what happens when a = b?
Click HERE for a GSP sketch that allows you to animate the above figure in order to observe what happens to the mean segments as "a" approaches "b."