

1. In this investigation we are asked to examine:
When we substitute n for 4 in the equation something very interesting happens when n=1.
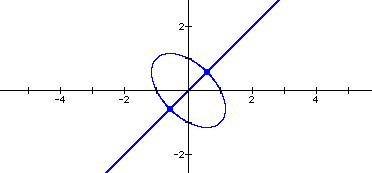
The graph looks like an ellipse centered at (0,0) with the line y=x running through it. As n grows large the graph disconnects at the intersection of the ellipse and the line. Also the graph becomes very curvy. As n gets very negative the graph looks as if it is trying to straighten out, however it is "pined down" at (0,1) and (0,-1). Here is a movie that will help to show exactly what I am describing.
What will happen when we decide to add a constant to each side of the graph?
When we add a constant to each side of the equation we will get different slices through the 3-dimensional surface given by the equation
Take a look at the graph of this surface.
