As b
changes...
Recall that in the original sine curve
y=sin x, a=1, b=1, and c=0. Let's explore what happens as the
value of b changes. Consider the following examples.
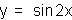
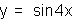
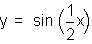
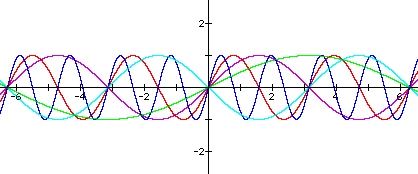
Focus on comparing the purple and the
red curves. The purple curve is simply y=sin
x. The red graph, y=sin(2x) demonstrates what happens when b=2.
Define a period as the length it takes
the curve to repeat the "wave cycle" of one crest and
one trough. In y=sin x, one cycle starts at the origin. Continuing
to the right along the x-axis, the cycle starts over again at
the point x = 
. Thus, the period of y=sin x is 
.
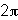In the graph of y=sin(2x), one cycle starts at the origin, but it ends
at the point x=
. Thus, the period for y=sin(2x) is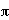 
.
By examining the remaining examples
we can determine that the period for a sine curve will be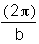 
.
Thus, for the graph of y=sin(0.5x), the
period will be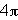 
because b=1/2.
What happens when b is negative? Take
a look at the graph of y=sin(-x). The curve is flipped or reflected over the
x-axis. So, in general, the graph of a sine curve with a negative
value of b is the graph of: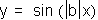
reflected
over the x-axis.