Proof:
The locus of the center of the common tangent
circle forms an ellipse.
The definition of an ellipse is that the set of all points
(x,y) in the plane such that the sum of the distances from (x,y)
to two fixed points if some constant. The set of all points (x,y)
refers to the path of points formed by the center of the common
tangent circle, which I will call C. So, we must show that the
sum of the distances from C to two fixed points is some constant
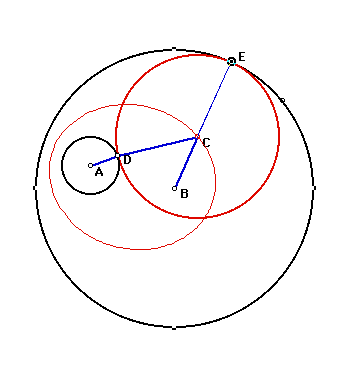
to prove that the locus is an ellipse. Consider the picture below.
Let circle A and circle B be the two original circles. A and
B are both fixed points as the centers of the two original circles.
The red circle C is one of the common tangent circles to both
circle A and circle B. Let AD be the radius of the small circle
A, and BE be the radius of the large circle B.
Two radii of the common tangent circle C are CD and CE. Thus,
CD = CE. Segment BE = BC + CE by segment addition. Since CD =
CE, BE = BC + CD by substitution. Thus, the distance from the
center common tangent circle C to the center of the large circle
B is equal to BC = BE - CD.
The distance from the center of the common tangent circle
C to the small circle A is equal to AC =
AD + CD.
We can solve for CD in the two green equations above, and
then set the resulting expressions equal to each other. Hence,
CD = BE - BC and CD = AC - AD. Thus, BE - BC = AC - AD. Rewritten:
AC + BC = BE + AD. Note that BE and
AD are the radii of our two original circles. The sum of the two
radii is a constant. Since A and B are fixed points, the red equation
tells us that the sum of the distance from C to two fixed points
is equal to some constant, namely the sum of the two radii. Therefore,
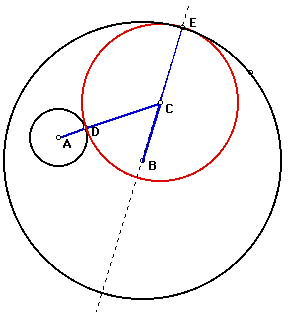
the path of points formed by C as E moves around the large circle
is an ellipse.