

For any triangle, several sets of segments are concurrent: the perpendicular bisectors of the sides, the angle bisectors, the altitudes, and the medians. This paper briefly presents proofs of theses four claims.
Theorem 1: The perpendicular bisectors of the sides of any triangle are concurrent.
The proof makes use of the following figure. Click anywhere on the figure to open Geometer's Sketchpad and explore.

Proof: Let XYZ be any triangle and points L, M, and N be the
midpoints of the sides as shown in the figure above.Construct
lines perpendicular to XZ at L and to YZ at M. These lines cannot
be parallel, for that would imply that segments XZ and YZ were
collinear. Call the intersection point C, as shown above.
Triangles CLX
and CLZ are congruent by the SAS congruence theorem so that CX
= CZ.
Also, triangles CLZ and CMY are congruent by the SAS congruence
theorem so that CZ = CY.
We must conclude that CX = CY, making triangle CXY isosceles.
Then CN is not only a median of triangle CXY, but also the perpendicular
bisector of XY.
Hence, all three
perpendicular bisectors of the sides of triangle XYZ are
concurrent at point C.
The proof is exactly the same if triangle XYZ is obtuse, causing point C to lie outside the triangle. You can explore this case in GSP by clicking on the figure above.
We get an added bonus by noting that point C is equidistant from X, Y, and Z. making C be the center of a circle through the vertices of the triangle. So we have a way to find the center of any circle: pick any three points on the circle and create the perpendicular bisectors of the segments that they determine. Click here to explore for yourself or here to run a script to demonstrate.
Theorem 2: The angle bisectors in any triangle are concurrent.
The proof makes use of the following figure. Click anywhere on it to open Geometer's Sketchpad and explore.
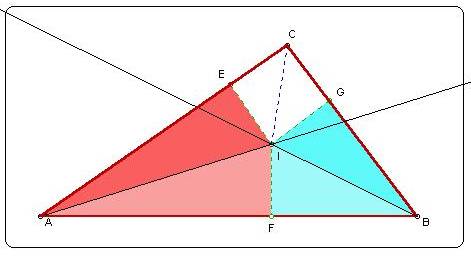
Proof: Let ABC be any triangle and construct angle
bisectors for angles A and B. These rays must intersect at some
point I as shown above. From I, construct perpendiculars to the
sides of the triangle, forming right triangles AIE,
AIF , BIF,
and BIG .
Triangles AIE
and AIF are congruent by the AAS
congruence theorem, so that IE = IF.
Also, triangles BIF and BIG
are congruent by the AAS congruence theorem, so that IF = IG.
We must conclude that IE = IG, making triangles CIE and CIG congruent
by the hypotenuse-leg congruence theorem.Then angles ICE and ICG
are congruent, implying that segment IC lies on the angle bisector
of angle C and that all three angle bisectors are concurrent at
point I.
We get an added bonus in that point I must be the center of a circle (with radius IE = IF = IG) that is inscribed in triangle ABC. Click here for a GSP script to draw an inscribed circle in any triangle.
Theorem 3: The altitudes in any triangle are concurrent.
The proof makes use of the following figure. Click anywhere on it to open Geometer's Sketchpad and explore.
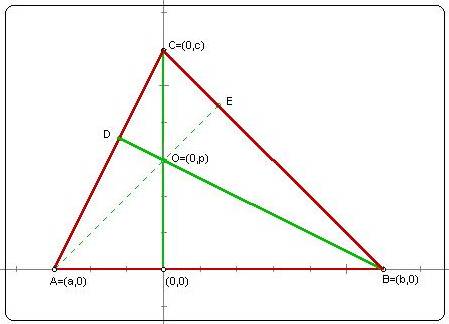
Proof: Locate any triangle ABC so that side AB lies along
the x-axis and the altitude from C lies along the y-axis as shown
above. The altitude from B must intersect the altitude from C
at some point with coordinates (0,p). Since BD is perpendicualr
to AC, the slope of BD is the negative reciprocal of the slope
of AC, so -p/b = a/c and b = (-pc)/a
If AE is the altitude from A and hence perpendicular to BC, then
the slope of AE must be b/c . Substituting for b shows the slope
of AE to be -p/a, implying that AE must pass through point (0,p).
Thus, all three of the altitudes of triangle ABC are concurrent
at O, a point called the orthocenter of ABC.
Theorem 4: The medians of any triangle are concurrent.
The proof makes use of the following figures. Click anywhere on the figure to open Geometer's SketchPad and explore.
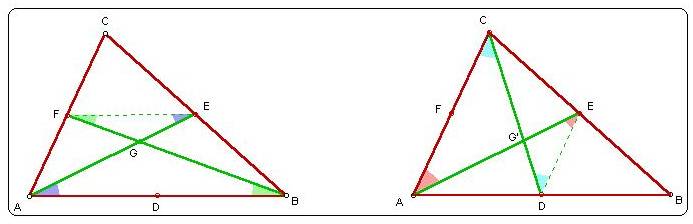
Proof: In any triangle ABC, construct the midpoints D, E, and
F of the sides as shown in the left figure above. Since EF is
parallel to AB, the green angles in the figure are congruent and
the blue angles are congruent, making triangles ABG and FEG similar.
Also, FE = .5 AB, so point G is located so that EG = .5
AG.
In the figure to the right above, an analagous argument leads
to the conclusions that triangles ACG' and EDG' are similar.
The big question is - are points G and G' really the same point?
Since ED = .5 AC, it must be true from similar triangles, that
EG' = .5 AG'. There is only one point on AE where that is true,
so G = G'.
Thus, the three medians of triangle ABC are concurrent at point
G.
Return to D Hembree's EMAT
6680 page
email to : dhembree@coe.uga.edu