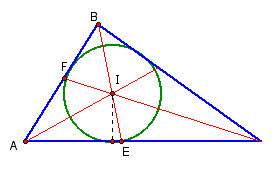
Prove: The angle bisectors of a triangle are concurrent.
Click here for a GSP 4.0 sketch to manipulate/investigate.

We wish to demonstrate that the angle bisectors of triangle ABC (rays BE, CF and AG) are concurrent.
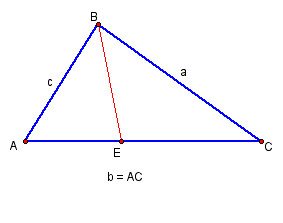
We will begin with a simplified figure. Since BE bisects angle ABC, angles ABE and EBC both equal one-half the measure of angle ABC. Then, by the law of sines,
Referring to the diagram at the top of the page, we could simlilarly show that
Therefore,
and by the converse of Ceva's theorem, we have demonstrated that the angle bisectors of triangle ABC are concurrent. This point of concurrency is known as the incenter. It is the center of the circle that can be inscribed in triangle ABC (tangent to all three sides).