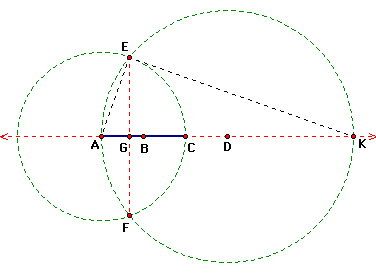
We wish to demonstrate that AC = 3AG.

Proof: Since B is the midpoint of AC, AB = BC. CD and BC are radii of the same circle, so CD = BC = AB, and AD = 3(AB). Note that AK = 2(AD) or 6(AB). In addition, radii AE and AC are congruent, so AE = AC.

Radius AE and tangent KE are perpendicular (if a tangent and a radius of the same circle intersect at a point on the circle, the tangent and the radius are perpendicular), so triangle AKE is a right triangle. GE is perpendicular to AK. We thus have similar triangles AGE and AKE.

Since triangles AGE and AKE are similar,

By substitution,

Simplifying: