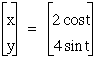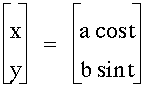
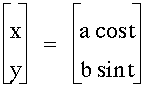
The following is a discussion of the graphs of the parametric equations

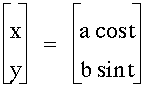
for various values of a and b.

If a = b, the equations will graph as a circle centered at the origin with a radius equal to a and b. For example, in the following graph, a = b = 2. Notice that the graph is a circle with a radius of 2.

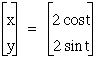
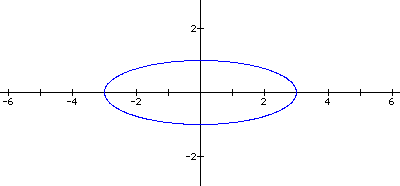
If the absolute value of a is greater than the absolute value of b, the resulting graph will be an ellipse centered at the origin with a horizontal (major) axis length of 2a and a vertical (minor) axis length of 2b. In the following example, a = 3 and b = 1. The resulting ellipse has a major axis length of 2(3) = 6 and a minor axis length of 2(1) = 2.

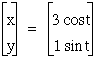
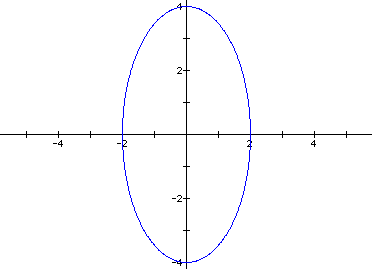
As we might expect, if the absolute value of a is less than the absolute value of b, the resulting ellipse will have a major axis length of 2b and a minor axis length of 2a. In the following graph, a = 2 and b = 4: