We want to study the following equation and its graph:
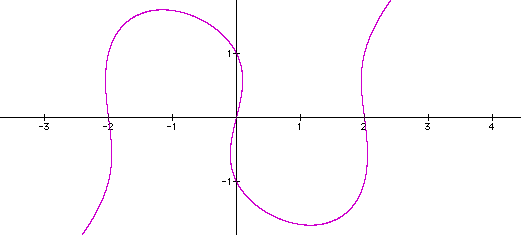
Now we want to look at what happens when we replace 4 with different values:
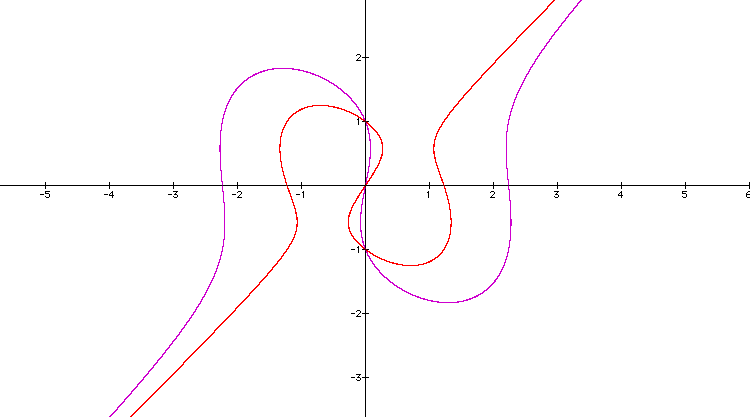
It is clear to see that for numbers >2 the graph widens along the x-axis and for numbers <2, the graph shrinks with respect to the x-axis. However, the roots along the y-axis remain the same which has to be true since we did not change the right hand side of the equation. If we continue to take numbers <2, at a certain point something different happens:
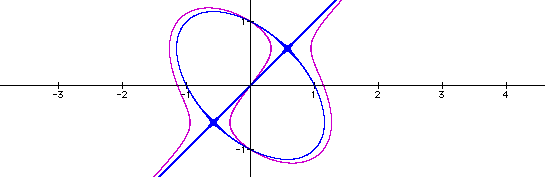
As we appoach the number 1, the graph continues to shrink with respect to the x-axis until we reach the number 1, when at that point the graph takes on a new configuration. This new shape still crosses the y-axis at 1,-1 as we would expect.
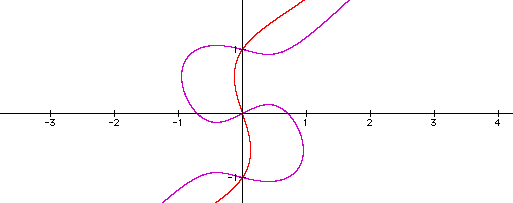
As we continue to use numbers <1, the graph again seperates and continues to shrink along the x-axes while maintaining it's roots on the y-axis.
Now let's investigate what happens when we carry the right side of the equation over to the left side and set it all equal to a constant like so:
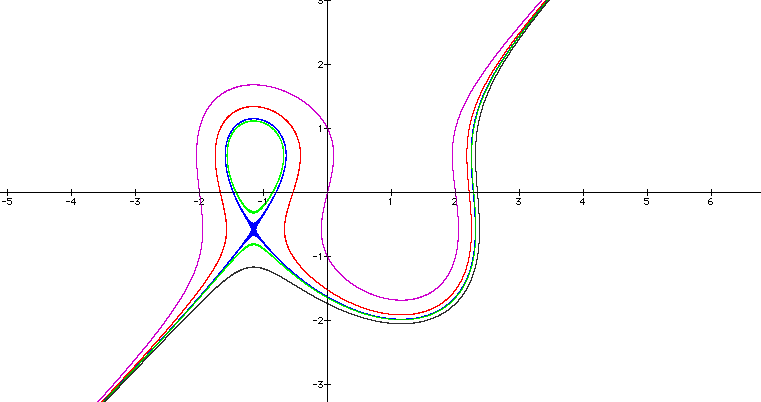
If we let the right side of the equation be a number >0, the left side of the graph will be inside -2 and the right side will be outside 2. Note something neat happens when our constant is a number between 2.5 and 3.5, the graph seperates into two pieces and then after 3.5 and reforms into a continuous graph. Also note that when we set the equation equal to a contant >0, our graph no longer crosses the y-axis at the points 1, -1, in fact, it now crosses the y-axis at only one point and that point will be < -1.
Lets take a look at one final graph:

This is the graph of our original equation using the x, y, and z axes. If you rotate the graph a little you can see it crosses each axis once and it looks like it has 2 negative roots(y and z) and one positive root(x).