4-4: Proving Lines Parallel
Using our prior constructions dealing with angles we
are going to construct parallel lines given a line and a point
not located on the line.
Step by Step Instruction
In order to construct parallel lines we need to start
with a line and a point not on the line
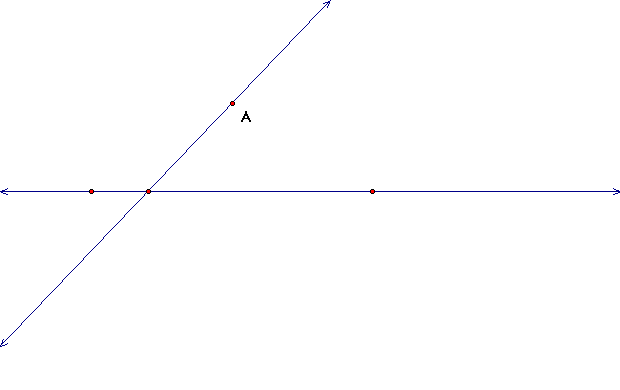
 a. Construct a line through point A that intersects
our given line
a. Construct a line through point A that intersects
our given line
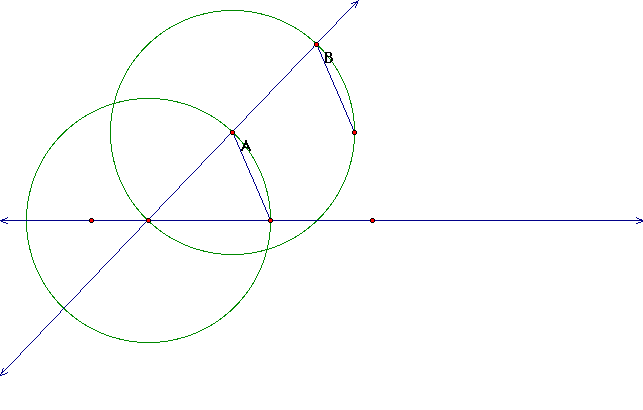
 b. Construct a circle with the vertex as the center
and point A as the point on the circle
b. Construct a circle with the vertex as the center
and point A as the point on the circle

c. Identify the point where the circle intercepts our given line
on the right of the transversal. Then construct a segment between
our given point and our newly identified point.

d. Now construct a circle with our center being point
A and our point on the circle being the vertex. The identify
the point where the circle intersects our transversal.

e. Lets now copy our segment from point A to our original
line to our most recent point on the transversal. To do this
we first highlight the line segment and the endpoints then from
the "Edit" menu select "Copy" then "Paste",
then move the new segment to where the top endpoint is directly
on top of the new point located on the transversal.
Now construct a line through points C and A this is
our line parallel to the given line.

There are several different postulates that can be
used to prove lines parallellet's use the postulates to show we
have an accurate construction by proving our lines are parallel
By Postulate 4-2, In a plane, if two lines are cut
by a transversal so that a pair of corresponding angles is congruent,
then the lines are parallel.
So we will measure corresponding angles,<BAC and
<ADE, to see if the are congruent

They are so based on Postulate 4-2, our lines are parallel
By Postulate 4-5, In a plane, if two lines are cut
by a transversal so that a pair of alternate interior angles is
congruent, then the two lines are parallel.
So let's measure the alternate interior angles, <CAD
and <HDA to see if they are congruent
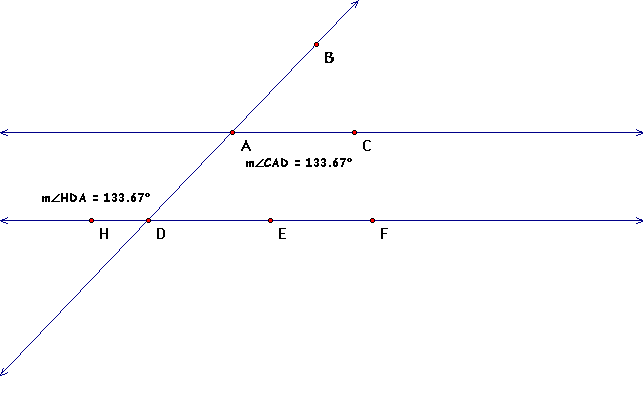
Therefore, since the angles are congruent that proves
our lines are parallel by Postulate 4-5
By Postulate 4-6, In a plane, if two lines are cut
by a transversal so that a pair of alternate exterior angles is
congruent, then the two lines are parallel
Let's measure <BAC and <IDH to test this postulate
with our construction

Yes, our construction fits Postulate 4-6; therefore
our lines are parallel
By Postulate 4-7, In a plane, if two lines are cut
by a transversal so that a pair of consecutive interior angles
is supplementary, then the two lines are parallel.
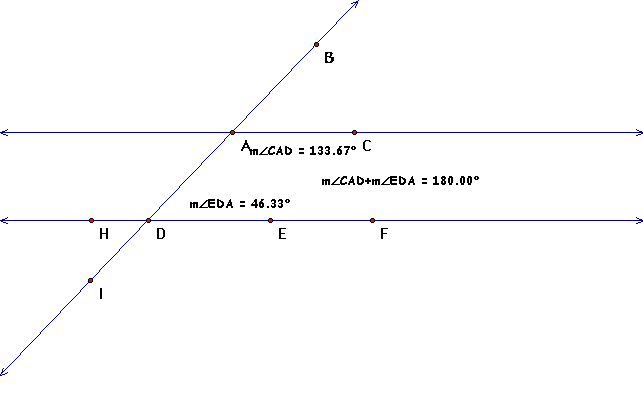
We'll measure the consecutive interior angles, <CAD
and <EDA, to test this postulate.

Adding our consecutive interior angles we get 180 degrees,
so yet again we have proven that our lines are parallel