Consider a triangle ABC as shown below:
First the altitude h from the vertex opposite c is constructed.
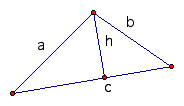
Now side c is divided into two sections, one of length x and the other of length c - x as shown.
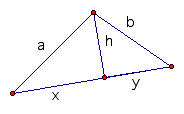
We can use the Pythagorean theorem to find h in terms of a, b, x, and y.
For the different parts of the triangle, we have that:
(1) 
(2) 
and
(3) 
by construction
Considering that the area = 
, then
the area squared = 
, so 
.
Rearranging equation (3) and substituting into equation (2) yields the following result:
Subtracting this result from equation (1) yields:
Rearranging equation (1) and multiplying through by 
yields
the following:
which factors into
where gives
the following:
which can be rearranged to yield:
Since 
, this equation becomes:
Factoring out the two's and dividing on both sides results in this equation:
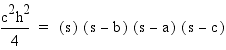
Taking the square root of both sides results in Heron's formula for the area of a triangle:
