
By Nami Youn

By Nami Youn
Write-up #2
Exploring
the graph of ![]()
Introduction
In this write-up, I examine the graphs of the graphs of ![]() using the different values of a. The focus is how the graph of
using the different values of a. The focus is how the graph of ![]() appears as a changes.
appears as a changes.
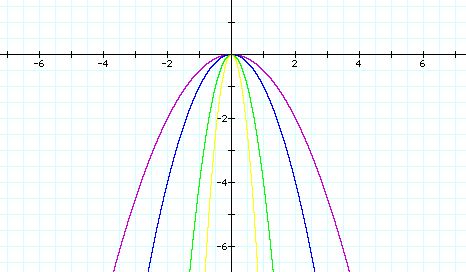
![]() (purple),
(purple), ![]() (blue),
(blue),![]() (green),
(green),![]() (yellow)
(yellow)

1) Let's notice the y values .
All the y-values is positive. The squaring operation
makes the result. Also, the parabola never touches the x-axis except at
the origin(0, 0).
2) Now, let's look at the shape of the graphs.
The parabola open up and has a minimum, when "a"
is positive.
3) Finally, notice that the
The graph of ![]() is wider than the graph
is wider than the graph ![]() .
Obviously,
.
Obviously, ![]() is wider than
is wider than ![]() .
.
Therefore. we can see that the graph becomes more narow
as the value of a increases, when a>0. Similary, the graph becomes
wider as the value of a decreases, when a>0.
![]() (purple),
(purple),![]() (blue),
(blue), ![]() (green),
(green), ![]() (yellow).
(yellow).
1) Let's notice the y values .
All the y-values is negaitive. Also, the parabola never
touches the x-axis except at the origin(0, 0).
2) Now, let's look at the shape of the graphs.
The parabola opens down and has a maximum, when a is
negative.
3) Finally, notice that the
The graph of ![]() is wider than the graph
is wider than the graph![]() . Obviously,
. Obviously,![]() is wider than
is wider than ![]() .
.
Therefore. we can see that the graph becomes more narow
as the value of a increases, when a<0. Similary, the graph becomes
wider as the value of a decreases, when a<0.
Let's compare of the following graphs.
![]() (purple),
(purple), ![]() (green)
(green)
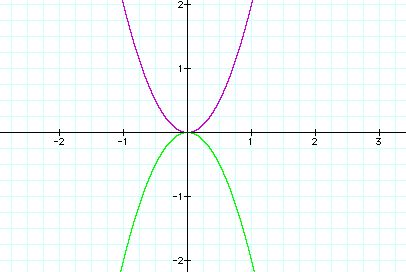
| -4 | -1 | 0 | 1 | 4 | |
| 16 | 2 | 0 | 1 | 16 | |
| -16 | -2 | 0 | -16 | -16 |
For the same x-value, y-absolute values of both of graphs
are the exactly same. This means that the graph ![]() is reflected over the x-axis. The axis of symmetry is x-axis.
is reflected over the x-axis. The axis of symmetry is x-axis.