By Nami Youn
Write-up #7
Tangent Circles

By Nami Youn
Tangent Circles
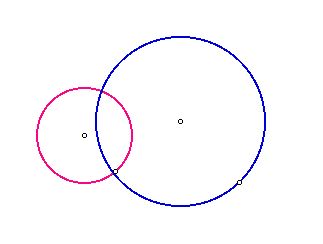
Given two circles and a point on one of the circles. We
construct a circle tangent to the two circles with one point of tangency
being the designated point D.
First of all, we should think of three cases accrding
to the position of two circles.
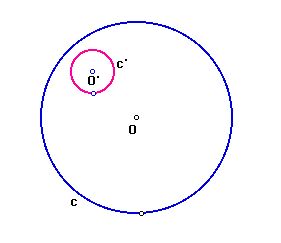
#1 Since the center of the desired circle will lie on
a line through O the center of the given circle c, we can constuct the
line through O.
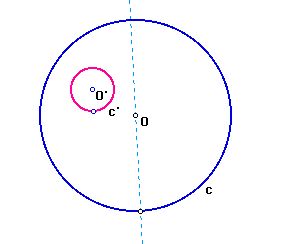
#2 We construct a circle centered at F, whose radius
is equal to the radius of c'. Connect the center of o' and an endpoint
of diameter of c''. Construct the perpendicular line to this segment.
Then the center of desired circle is the intersection point of a perpendicular
bisector of pink segment and the blue lay.
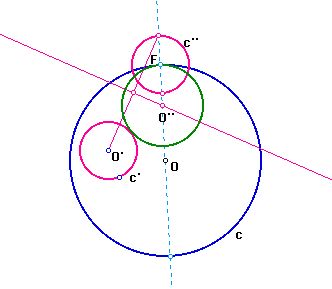
O'O'' + O'O = radius of c' + radius of c = constant.

Click here for a GSP sketch to
see a trace of the line as the tangent point of the constructed circle
moves around the large circle. An envelope of lines is
produced all tangent to the ellipse.
The center of the desired circle will lie on the line
through the center of the given circle c'.
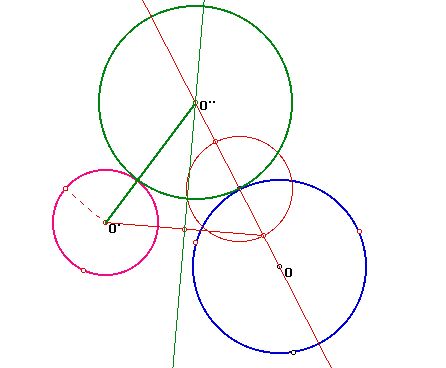
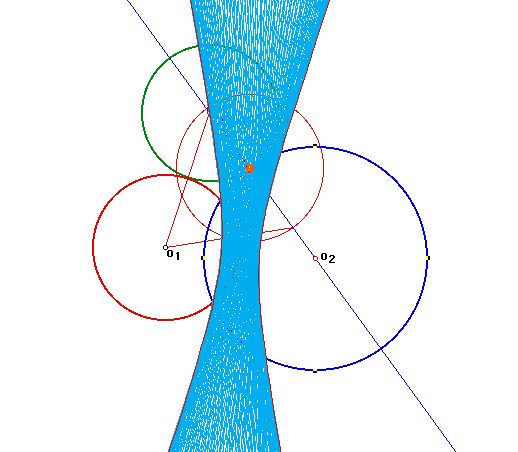
We can see O'O'' - OO'' = radius of c + radius of c' =
constant.
Therefore, the locus of the centers of the tangent circles
is
an hyperbola
with foci at the centers of the given circles.
Click here for a GSP sketch.