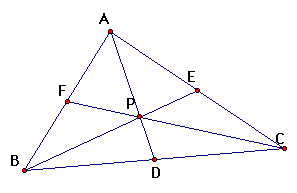
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersection with the opposite sides in points D, E, and F respectively.
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and locations of P.

First we'll look at medians of a triangle where P is the centroid. Notice that
(AF)(BD)(EC) = (FB)(DC)(EA) and their ratio equals one.

Now, we'll take a look at the angle bisectors of a triangle:
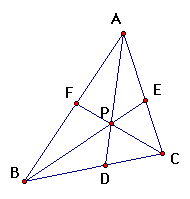
And yes, (AF)(BD)(EC) = (FB)(DC)(EA) and their ratio equals one.

What about any arbitrary P, you say?
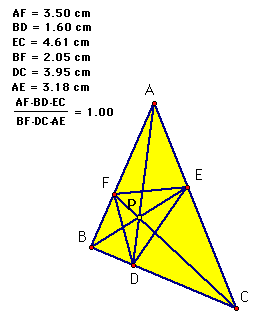
And yes again, (AF)(BD)(EC) = (FB)(DC)(EA) and their ratio equals one! Hmmm...makes you wonder!
B. Conjecture? Well, it seems for a point P for our given triangles ABC that (AF)(BD)(EC) = (FB)(DC)(EA) and their ratio equals one.
Can we prove that? Sure!
Proof:
Extend the lines BE and CF beyond the triangle until they meet GH, the line through A parallel to BC. There are several pairs of similar triangles: AHF and BCF, AGE and CBE, AGP and DBP, DCP and AHP.
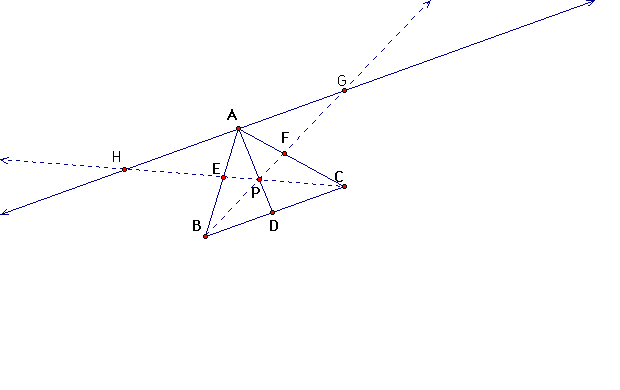
From these and in that order we derive the following proportions:
AF/FB=AH/BC (#)
CE/EA=BC/AG (#)
AG/BD=AP/DP
AH/DC=AP/DP
from the last two we conclude that AG/BD = AH/DC and, hence,
BD/DC = AG/AH (#)
Multiplying the identities marked with (#) we get
AF/FB*BD/DC*CE/EA = AH/BC*BC/AG*AG/AH = (AH*BC*AG)/(BC*AG*AH) = 1
Therefore, if the lines AD, BE and CF intersect at a single point P, the identity (1) does hold. Which is to say that the fact of the three lines intersecting at one point is sufficient for the condition (1) to hold. Let us now prove that it's also necessary. This would constitute the second part of the theorem. In other words, let us prove that if (1) holds then AD, BE, CF are concurrent.
Indeed, assume that P is the point of intersection of BE and CF and draw the line AP until its intersection with BC at a point D'. Then, from the just proven part of the theorem it follows that:
AF/FB*BD'/D'C*CE/EA = 1
On the other hand, it's given that
AF/FB*BD/DC*CE/EA = 1
Combining the two we get
BD'/D'C = BD/DC or
BD'/D'C + 1 = BD/DC + 1 or
(BD'+D'C)/D'C = (BD+DC)/DC
Finally
BC/D'C = BC/DC
which immediately implies D'C=DC. That is, D' and D are one and the same point.
End of Proof!
Can the result be generalized (using lines
rather that segments to construct ABC) so
that the point P can be outside the triangle? Of course!
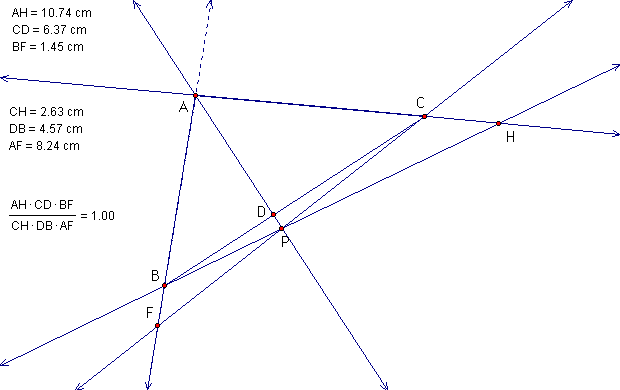
Here's a GSP Sketch so you can see for yourself!
C.Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4? When is it equal to 4?
Let look at when P is the centriod...

...the ratio equals 4! Click here
for a GSP Sketch
What about the ratio for the angle bisectors?
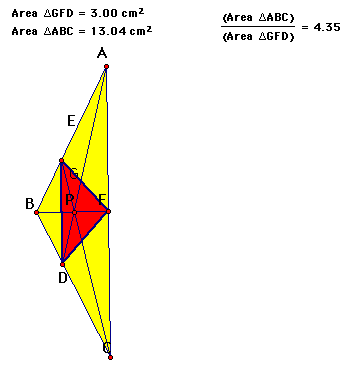
It's always greater than 4? Check it out!
Another angle bisector triangle!

Finally, for an arbitrary P!

It's ratio is also always greater than 4! Don't believe it?
Check out the GSP sketch!
References
www.mtl.math.uiuc.edu/modules/dynamic/lessons/lesson3.html
http://mcreafamily.com/MathHelp/GeometryTriangleCevaTheorem.htm
Geometry: Ancient and Modern. Silvester, John