Cooled Data:
A Long Study of Watching
Boiling Water Cool
In this assignment,
I took a cup of boiling water and measured its temperature every
minute for 30 minutes. I am going to attempt to come up with a
function that will model the data. I did the experiment twice
to see how much of a difference there would be depending on the
size/shape of the container used. I first used a pan that had
a diameter of 6.5 inches and a depth of 0.5 inches giving a volume
of approximately 16.6 cubic inches and a surface area of 33.2
square inches. Next, I used a mug that had a diameter of 3 inches
and a depth of 2 inches giving a volume of approximately 14.1
cubic inches and 7.1 square inches.
First, let's look at
the data from the pan of boiling water:
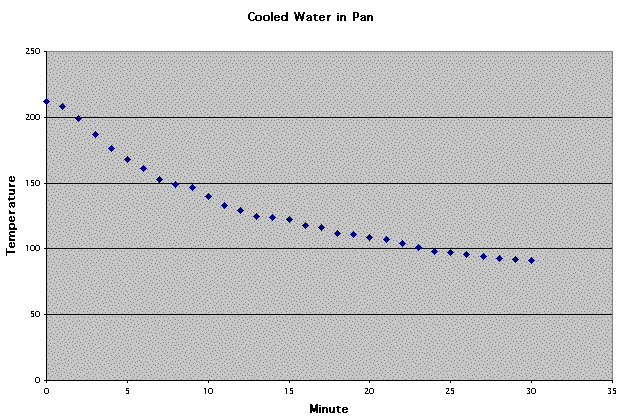We can use Newton's
Law of Cooling to find an equation that fits the data.
Newton's Law of Cooling
states:
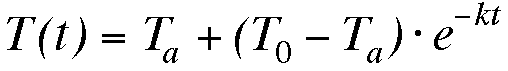where
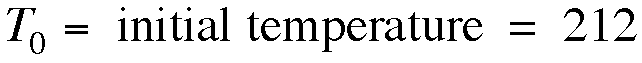
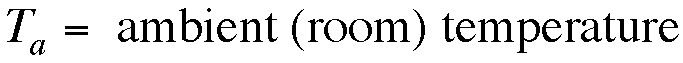t = time in minutes
k = constant
In the data above,
the room temperature was 70 degrees. In order to find the constant,
k, I took two of my corresponding data values, plugged them into
the equation, and solved for k. I then took the average of those
two k-values to get a more accurate value of k. Therefore, my
equation is:
Now, I am going to
use this function to predict the temperature after 45, 60, and
300 minutes.
T(45) = 77
T(60) = 72
T(300) = 70
Click
here to see an Excel file showing my
temperature reading compared to the temperature yielded in the
formula. Then, you will see the square of each difference for
each time in its own column. Then, those squares are summed and
divided by 31 (there are 31 data points from t = 0 - 30) giving
the standard deviation to be 7.16 (which seems to be very high
-- I was hoping for a better fit).
Just for fun, I used Maple to find
a polynomial of degree 6 to fit my data. I used seven data points
that correspond to t = 0, 5, 10, 15, 20, 25, & 30 minutes
and used the "interp" command to get the following polynomial:
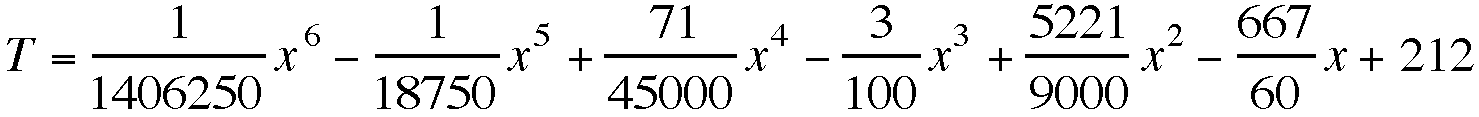The polynomial looks pretty messy but
it is a good fit for several data points.
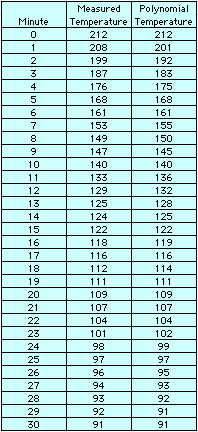The main problem with this polynomial
is that as time gets larger, my temperature should approach 70.
This polynomial apparently curves upward above t = 30 because
I got extremely large values for the temperature when plugging
in 35, 40, and 45 minutes. For example, this polynomial gives
a temperature of 686 degrees for time = 45 minutes which is obviously
incorrect. It was fun to try!
The following table and chart accompany
the experiment when done with a coffee mug as described. I wanted
to see how much of a difference there would be when a different
container was used.
From the data, we can see a significant
difference in the time it took for the water to cool in the mug
compared to the pan. We can deduce that the larger the surface
area of the water, the quicker it cools.
Return