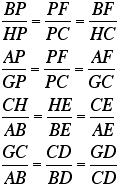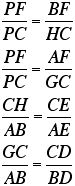Final Assignment!!
The final assignment
for EMAT 6680 involves a triangle and an arbitrary point inside
the triangle. We are going to explore some ratios that come out
of this sketch and hopefully prove why the ratios are what they
are. The following GSP sketch was made by constructing a triangle,
that arbitrary point P, and the lines through the point and the
vertices.
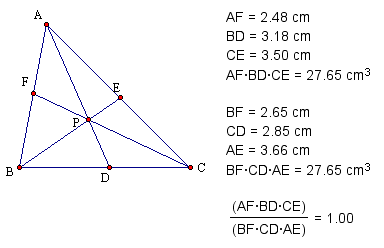 What do you know? The ratio is 1!
Click
here to drag point P in the GSP sketch
to see if it is always one.
What do you know? The ratio is 1!
Click
here to drag point P in the GSP sketch
to see if it is always one.
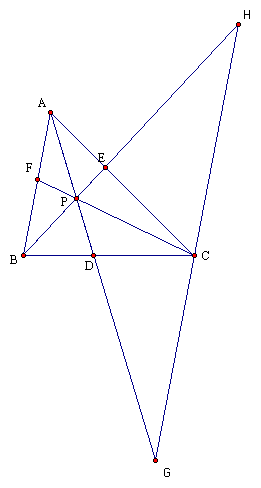 I have constructed a line through vertex
C that is parallel to segment AB. Then, I extended the line segments
through the other two vertices until they intersected my new line
GH. We now have similar triangles in BPF and HPC, APF and GPC,
CHE and ABE, and GCD and ABD using the Angle-Angle Theorem for
similar triangles because the vertical angles are congruent and
the alternate interior angles congruent. Since corresponding sides
of similar triangles are in proportion, we have the following
proportions:
I have constructed a line through vertex
C that is parallel to segment AB. Then, I extended the line segments
through the other two vertices until they intersected my new line
GH. We now have similar triangles in BPF and HPC, APF and GPC,
CHE and ABE, and GCD and ABD using the Angle-Angle Theorem for
similar triangles because the vertical angles are congruent and
the alternate interior angles congruent. Since corresponding sides
of similar triangles are in proportion, we have the following
proportions:
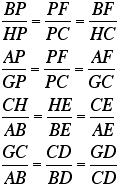 Now, you may ask what in the world
are all of these proportions going to do for us? We don't need
all of them, just these:
Now, you may ask what in the world
are all of these proportions going to do for us? We don't need
all of them, just these:
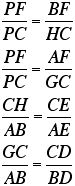 Using simple laws of proportions, we
see that
Using simple laws of proportions, we
see that
 .
From the first of these ratios, we
have a new ratio:
.
From the first of these ratios, we
have a new ratio:
 .
Now, using some fancy footwork and
substitution of equivalent ratios, we end up with the following
proportion:
.
Now, using some fancy footwork and
substitution of equivalent ratios, we end up with the following
proportion:
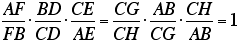 Therefore, the ratio will always be
one!
I did get some help with this proof.
Click
here to view the web page and proof.
Next, I want to look at this ratio
if point P is outside the triangle. Does the generalization hold?
Therefore, the ratio will always be
one!
I did get some help with this proof.
Click
here to view the web page and proof.
Next, I want to look at this ratio
if point P is outside the triangle. Does the generalization hold?
 Click
here to drag point P to see if the
ratio will always be one.
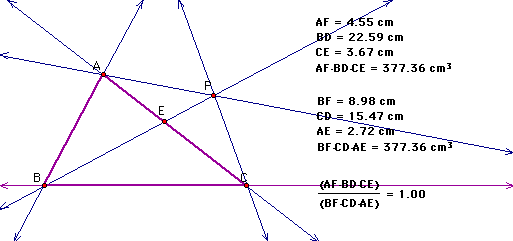
For my last trick, I am going to show
that the ratio of the areas of triangle ABC and triangle DEF is
always greater than or equal to 4.
Click
here to drag point P to see if the
ratio will always be one.
For my last trick, I am going to show
that the ratio of the areas of triangle ABC and triangle DEF is
always greater than or equal to 4.
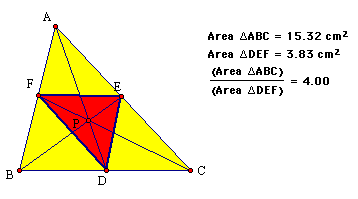 Apparently, the ratio of the areas
is equal to 4 if point P is the centroid of the circle. If P is
not the centroid, the ratio is greater than 4. Click
here to drag point P in a GSP sketch to see that this is always
true.
Apparently, the ratio of the areas
is equal to 4 if point P is the centroid of the circle. If P is
not the centroid, the ratio is greater than 4. Click
here to drag point P in a GSP sketch to see that this is always
true.
Return