Given triangle ABC. Construct the Orthocenter
H. Let points D, E, and F be the feet of the perpendiculars from
A, B, and C respectfully.
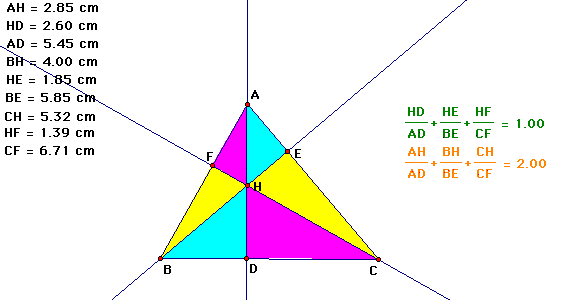
Through the investigation we can assure
two resuls the above for acute triangle.
Let me show an example.
PROOF)
We can represent an area of the triangle above as three defferent
formulas.
Area of ABC = (BC * AD)/2
Area of ABC = (CA * BE)/2
Area of ABC = (AB * CF)/2
And
Area ABC = Area HBC + Area HCA + Area HAB
Area HBC = (BC*HD)/2
Area HCA = (CA*HE)/2
Area HAB = (AB*HF)/2
Therefore
2 * AreaABC = BC*HD + CA*HE + AB*HF
BC*AD = BC*HD +
CA*HE + AB*HF
Now we can get the first result by the following steps
1 = (BC*HD)/(BC*AD)
+ (CA*HE)/(BC*AD) + (AB*HF)/(BC*AD)
By three different area formulas BC*AD
= CA*BE = AB*CF
1 = (BC*HD)/(BC*AD)
+ (CA*HE)/(CA*BE) + (AB*HF)/(AB*CF)
That is,
HD/AD + HE/BE + HF/CF = 1
Second proof can be directly induced from the first result.
HD = AD - AH
HE = BE - BH
HF = CF - CH
Let's put these equations into the first result.
(AD- AH)/AD + (BE - BH)/BE + (CF-CH)/CF = 1
1 - AH/AD + 1 - BH/BE + 1 - CH/CF = 1
3 - (AH/AD + BH/BE + CH/CF) = 1
That is,
AH/AD + BH/BE + CH/CF = 2
Further study
What if the triangle
is right?
 Orthocenter is to be a point B and so our B, D, F,
H are coincidence.
Since HD=0, HF=0, BE=HE,
HD/AD + HE/BE + HF/CF = 1
And since BH=0, AD=AH, CF=CH,
AH/AD + BH/BE + CH/CF = 2
What if the triangle
is obtuse?
Orthocenter is to be a point B and so our B, D, F,
H are coincidence.
Since HD=0, HF=0, BE=HE,
HD/AD + HE/BE + HF/CF = 1
And since BH=0, AD=AH, CF=CH,
AH/AD + BH/BE + CH/CF = 2
What if the triangle
is obtuse?
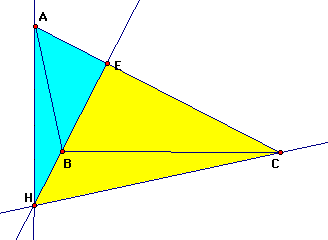 More detail figure is the following
More detail figure is the following
 From this figure we can know that our two results are
not satisfied for the obtuse.
From this figure we can know that our two results are
not satisfied for the obtuse.
Return to
Hyungsook's homepage





