Investigation:
1) I looked at the different graphs of the equation
![]()
I varied a as follows: 1, 2, -1, 3, 1.5, -1.5, and 0.25

I noticed that as a increases, the graph begins to look more and more like a circle.
This time, I kept a as a constant 1 and varied b as follows:
1, 2, -1, -2, 0.5, and 0.25.
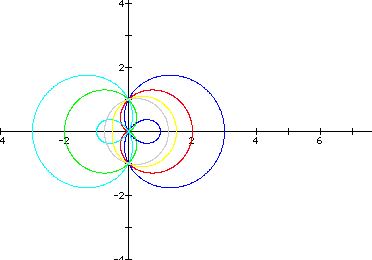
I notice that the graphs when b=2 and b=-2 are reflections of each other along with b = -1 and b = 1.

Looking at the four graphs in which b is greater than 0, we can see this time that as b decreases, the graph takes on a more circular shape.
This time, I will fix a and b and change k.
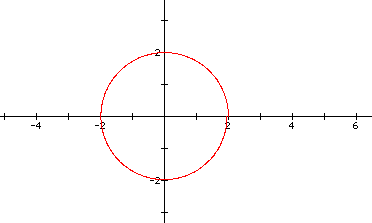
Here, k = .05. The graph looks like a circle, but if we look closer around theta equaling 2, we can see that the circle is not closed. There is a slight opening.

and expanding the domain of theta to 1000, gives us the following:
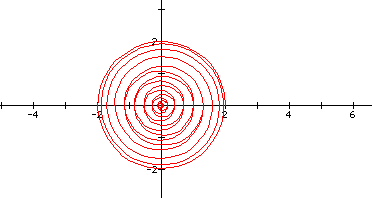 .
.
(this was an interesting side-thought). If we were to look again at fixed a and b, and change k, we would see the same sort of pattern seen with changing a and b. As k gets smaller, the graph takes on a more circular shape.
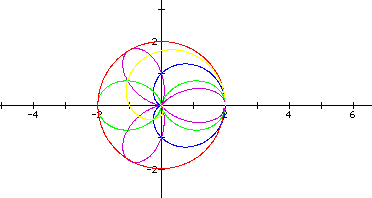
If we look closely at the graphs with k = 1, 2, and 3, we can see a pattern with the number of petals on the graph.

For k = 100, we have the following:
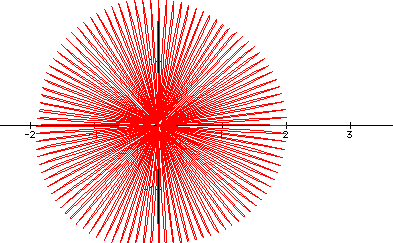
with 100 petals ( we can assume).
Now we can compare the following two polar equations:
![]() and
and
![]() . For fixed values of a,b, and
k, we get the following graphs:
. For fixed values of a,b, and
k, we get the following graphs:

The equation for the graph
in purple is ![]() , while the equation for the graph
in green is
, while the equation for the graph
in green is ![]() .
.
If we vary k, we can
see something very different. Above, as k varied in the
original equation, we saw that the number of loops in the graph
corresponded to the value of k. This does not appear to
be the case with ![]() .
.

In this case k = 2.

In this case k = 3. If this pattern follows, the number of petals for k, even, should be twice k, for k odd, the number of petals should be equal to k.