The notion of variable is an important foundation to lay during the elementary schooling years. Children need experiences involving unknown quantities. It is appropriate and common to use shapes as a representation of variables when dealing with children. They need to have opportunities to discover the main concept of variable; that in a given situation the value of a variable remains constant no matter how many times it is used. It is also important for children to have experiences in reasoning with multiple variables and have opportunities to reason about the values of these variables in relationship to each other.

This link will allow you to download the GSP file circles and squares.GSP which was designed by Daniel Scher as a part of the Sketchpad for Young Learners project. This sketch involves using arithmetic reasoning to determine the secret values of the circle and square in as few turns as possible.

My particular style of teaching in working with my PST is to model for them / with them, activities using approaches similar to those I might make while working with children. The largest differences between my work with PST and children being in the extension activities I use, the types of numbers that I choose, and the level of questioning involved in the activity.

Introducing the sketch

I begin with a whole group example using the sketch. This approach is important for me to model the type of discourse and discussion that is appropriate during whole group instruction with technology. I understand that there will be times when not all students can be on their own computer, and for my PST it is important for them to see that technology can be effectively employed even when it seems you do not have enough resources.

Using the default secret values of the circle and square, I will model a systematic approach to finding the secret values. I'll have a student select one of the configurations and I'll drag it into the playing area, this will expose the total value of the group of shapes. Suppose that we realize that = 8. Understanding that each square has equal value, and is a positive integer, I'll have students give me all of the possibilities for the values of circle and square. In this case

Students should keep track of these on paper. Next we'll choose a second configuration and drag it over. Suppose this time we see that= 9. The students should give the possibilities as:

From these two combinations we can see that square = 3 and circle = 2 should be the solution. An important question to ask here is How do we know this must be the solution? This can lead to a discussion with PST towards simultaneous equations. Another option to use with both PST or with children is to decide that we think that the solution is square = 3 and circle = 2 and predict another shape configuration as a check. This can lead to an informal discussion of proof with children.

Activities

The main activity to be used with this is just to play the game. Try to find the secret values in as few turns as possible. For my PST, what I'd like them to get from playing the game is to develop a method similar to the elimination method used in solving simultaneous equations. If they choose two configurations such as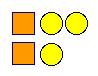they should realize that since each has one circle and one square, that the value of the circle can be deduced, and then using substitution the value of the square can also be found. My approach would be to have them play the game in pairs for 10 minutes or so, taking turns choosing values and determining them in as few turns as possible. Then being them back together for a whole class discussion of their methods. A point to be made during this time is what it might take to get children to come up with this approach. One thought on this is to do a whole class discussion with the teacher modeling the strategy and having the children try and find the pattern to the teacher's approach.

This sketch can be used in conjunction with my balance activity page to allow for some great experiences in algebraic reasoning with both PST and children.

Return to Pre-Algebra Page