Dynamic software such as GSP is exceptionally useful when examining and exploring isometric transformations. While my PST have experience thinking about "flips, slides, and turns", I try get them to think more about "reflection, translation, and rotation". Using a simple picture, we explore each transformation, their defining characteristics, and also try to make geometric connections within the construction of each isometry of the plane. I feel that this deeper exploration of transformations (with much more information than elementary students need to know) will help give my PST the confidence to let their students explore on their own in this topic area.
This page contains the lesson plan that I use with my PST. It is more of a skeletal plan than one that is very detailed and formal. I like to leave it open to encourage discussion within the classroom, and I make note of the types of questions I want to cover and important ideas that need to come out during the discourse.
You can click on this link to download the file stick dude.gsp . This is a sketch I made and use to demonstrate and explore isometries. If you have more time, or if your students need some more hands-on time with GSP, you could also have them create their own stick figure to use during the exploration.
Transformations
I open this lesson with a quick discussion of what transformations are and a recap of the three main isometries of the plane. I make sure to talk about them using kid terms [flips, slides, and turns] as well as the formal mathematical terms. Usually when we have this talk, the PST make some amusing and expressive hand motions along with their explanations of the transformations of the plane. I always comment on this and tie it to the inherent sense of movement that accompanies transformations. We want children to experience these actions and be able to see the motions involved. This helps to set the need for using a dynamic environment to explore these topics.
I try to let my PST lead the exploration of each of these transformations as much as possible. I will model the order in which I think things should be introduced, try and ask questions that will lead them to think about other connecting ideas, and in general act as the facilitator instead of approaching this content in a lecture style. along the way, I'll point out some of the special features and tools of GSP that allow us to facilitate the exploration more easily.
I approach each transformation by asking for the defining characteristics. I'll then talk about how to use GSP to perform the transformation. I'll give them some time to do some free exploring with the transformed object to describe the way the image and pre-image change when different things [like the defining characteristics] are moved around the screen. From this exploration, I want them to make some hypothesis about what is actually happening and to think about how they might describe it geometrically. Where needed, I'll pose some of the questions listed in each section to help them along in the process. As a group we will come to describe the geometric constructions of each transformation.
Flips (reflections)
Q: What defines a reflection?
Process
1. Draw a vertical line anywhere
on the screen.
2. Select that line and mark as mirror (also show double click
as short cut)
3. Highlight "dude" and reflect.
Possible exploration questions
Q: Move line horizontally, what do you notice?
Q: Select one point and rotate the line, what happens here?
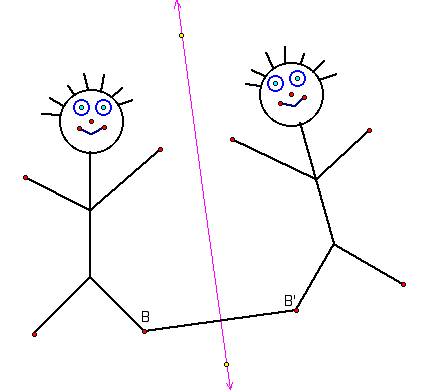
Have students select one pair of points [image and pre-image] and draw segment.
Mark intersection of mirror and measure distance from points to mirror.
What do you notice? Reminder, or question: How is distance measured? [Perpendicularly]

From this exploration, the PST should conclude that the mirror acts as a perpendicular bisector of every segment connecting a point on the image with its preimage point.
Slides (translations)
Q: What defines a translation?
1. Open, refresh stick dude.
2. Draw line segment and label points.
3. Demonstrate how to mark as vector. [What is a vector? Can someone
express it another way?]
4. Select dude and translate.
Possible Exploration Questions:
Q: Move one of the endpoints of the vector, what happens? [Image
is same distance and direction from pre-image.]
Have students justify observation by measuring distances between vector and segment from pre-image to image.
Q: How can we express "the
same distance" - what does that mean about the segments?
[Congruent - the same length]
Q: How can we express "the same direction" - how do
we describe this in terms of lines and segments? [Parallel]
Q: So we have two segments that are both congruent and parallel
and opposite to each other, what geometric figure does this describe?
[Parallelogram]
Have students draw in the rest of the parallelogram and manipulate
it around observing the figure.
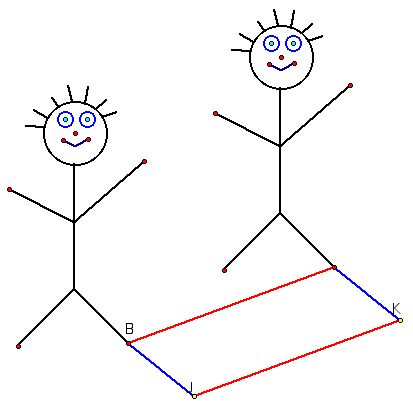
The fact that the parallelogram is the geometric construction that allows us to create translations the important idea I want the PSt to take away from this section.
Turns (rotations)
Q: What defines a rotation?
1. Refresh dude.
2. Choose a rotation point "C."
3. Mark "C" as center.
4. Select dude and rotate 90 degrees (fixed angle).
Q: What happens? [Difficult to tell from this situation.]
Have students construct the triangle between center, image, and pre-image and measure sides and angle. [Isosceles, right triangle] Have them move again. What happens?
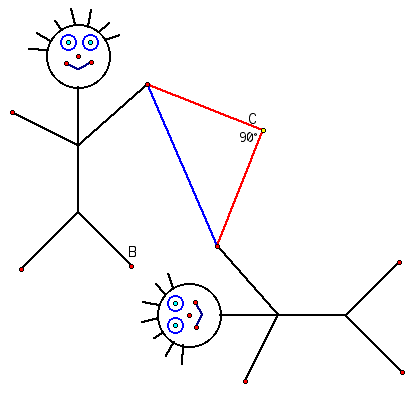
Have students delete C - this will clear the image. Why?
Have them select a new center and also draw an angle on their screen. Have them mark the angle and use it to perform the rotation.
Have them reconstruct the same
triangles and measure the sides and angles to realize that the
angles and distances are fixed in a rotation.
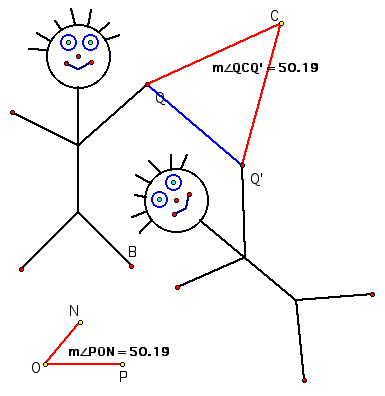
I want the PST to see that the construction of a rotation is an isosceles triangle with the vertex angle of the triangle being the angle of rotation.
This exploration with GSP that reveals the geometric constructions behing the different transformations. A possible next step in this topic is to use isometric dot paper, or straight edge and compass to have students create these same constructions by hand. In a content course this is something I would most certainly want to do, in my methods class I do not pursue these activities.