
Assignment 9
Pedal Triangles
By Carly Coffman
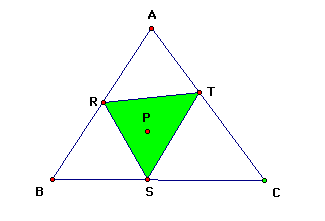
Let triangle ABC be
any triangle. Then, if P is any point in the plane, then the triangle
formed by constructing perpendiculars to the sides of ABC (extended
if
necessary) locate three points R, S, and T that are the intersections.
Triangle RST is the Pedal
Triangle for Pedal
Point P.
 Click here to explore.
Observations:
Click here to explore.
Observations:
- When the pedal point,
P, is located outside triangle ABC, the pedal triangle vertices
become colinear when two of the pedal triangle vertices are at
two of triangle ABC's vertices.
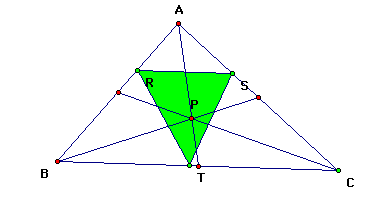
Pedal Point as the
Centroid
First, we will explore what
happens to the pedal triangle when the pedal point, P, is the
centroid. The centroid is the intersection of the midpoints
of the sides of a triangle.
 Click here to explore.
Observations:
Click here to explore.
Observations:
- When triangle ABC is isosceles,
the pedal triangle is isosceles.
- The pedal point, P, does
not go outside of triangle ABC.
- When the vertices of the
pedal triangle are at the midpoints of the sides of triangle
ABC, the pedal triangle is equilateral.
- When a vertex of the pedal
triangle is at the vertex of triangle ABC, the pedal triangle
only exists when the vertex angle of triangle ABC angle is a
right or obtuse angle.
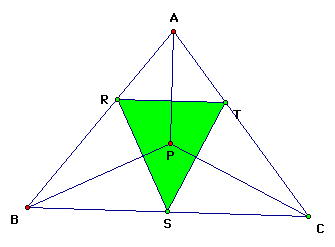
Pedal Point as the
Incenter
Secondly, we will explore what
happens to the pedal triangle when the pedal point is the incenter.
The incenter is the intersection of the angle bisectors
of a triangle.
 Click here to explore.
Observations:
Click here to explore.
Observations:
- When triangle ABC is isosceles,
the pedal triangle is isosceles.
- When triangle ABC is a
right isosceles triangle, the pedal triangle is isosceles.
- When triangle ABC is equilateral,
the pedal triangle is equilateral.
- The vertices of the pedal
triangle will not reach the vertices of triangle ABC until the
degenerate case (triangle ABC becomes a line).
- The pedal point does not
go outside of the triangle.
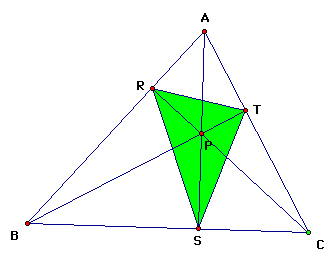
Pedal Point as the
Orthocenter
Thirdly, we will explore what
happens to the pedal triangle when the pedal point is the orthocenter.
The orthocenter is the intersection of the triangle altitudes
at the vertices.
 Click here to explore.
Observations:
Click here to explore.
Observations:
Notice that the pedal triangle
is the orthic triangle when the pedal point is the orthocenter.
Let's look at the definitions of the triangles to see why this
is true.
Definitions:
- Orthic Triangle - triangle
formed by the intersections of the altitudes of a triangle from
the vertices
- Pedal Triangle - triangle
formed by the intersections of the lines perpendicular to the
sides and the pedal point
Since the pedal point is the
orthocenter, the altitudes of the triangle at the vertices are
on the line that is perpendicular to the sides through the orthocenter,
or pedal point. Therefore, when the pedal point is the orthocenter,
the pedal triangle is the orthic triangle.
- When triangle ABC is isosceles,
the pedal triangle is isosceles.
- When triangle ABC is a
right triangle, the pedal triangle vertices become colinear.
- When triangle ABC is obtuse,
the pedal point exists outside triangle ABC.
- When triangle ABC is obtuse,
the vetices of the pedal triangle are colinear.
- When triangle ABC is equilateral,
the pedal triangle is equilateral.
- The only instance where
a vertice of the pedal triangle is at a vertex of triangle ABC
is when triangle ABC is a right triangle.
Pedal Point as the
Circumcenter
Fourthly, we will explore what
happens to the pedal triangle when the pedal point is the circumcenter.
The circumcenter is the intersection of the perpendicular
bisectors of the sides of a triangle.
 Click here to explore.
Observations:
Click here to explore.
Observations:
- When the pedal point is
at the circumcenter, the vertices of the pedal triangle are the
intersections of the perpindicular bisectors of the triangle
sides.
- The pedal triangle is
similar to triangle ABC since the vertices of the pedal triangle
are the midpoints of the sides of triangle ABC. Angle BAC is
congruent to angle TSR, angle ACB is congruent to angle TRS and
angle CBA is congruent to angle STR.
- The pedal point, P, exists
outside triangle ABC when triangle ABC is obtuse.
- The pedal point, P, exists
on a side of triangle ABC when triangle ABC is a right triangle.
- The pedal point, P, exists
inside triangle ABC when triangle ABC is acute.
Pedal Point on the
Sides
 Click here to explore.
Observations:
Click here to explore.
Observations:
- Notice that the pedal
point, P, becomes the pedal triangle vertex, R. If you were to
place the pedal point on the side AC, P would be the same point
as T. If you were to place the pedal point on the side BC, P
would be same point as S.
- As the pedal point moves
along the side of triangle ABC, the angle TPS stays the same
measure.
- When P is placed at the
vertex A or at the vertex B, the pedal triangle becomes degenerate
(triangle becomes a line).
- When triangle ABC is a
right triangle, the pedal triangle is a right triangle also.
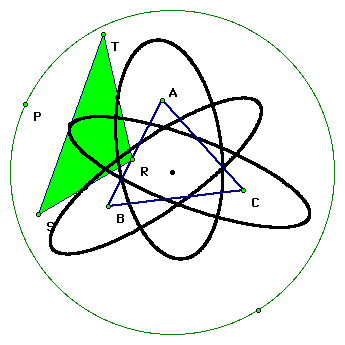
Exploration
Locate the midpoints of
the sides of the Pedal Triangle. Construct a circle with center
at the circumcenter of triangle ABC such that the radius is larger
than the radius of the circumcircle. Trace the locus of the midpoints
of the sides of the Pedal Triangle as the Pedal Point P is animated
around the circle you have constructed. What are the three paths?
GSP Solution
We get three elliptical
loci from the midpoints of the pedal triangle.
Return to Home Page








