The Tomahawk

Carly Coffman

 

 

When looking through the book Geometrical Tools:  A Mathematical Sketch & Model Book by Robert C. Yates, I came across a tool called the “Tomahawk”.

 

How to Construct The Tomahawk (using GSP 4.03)

 

1)    Construct the semicircle BOC such that BO = OC

Ø     Using the segment tool, construct segment BC (label endpoints B and C)

Ø     Highlight BC and choose “Midpoint” under construct (label as point O)

Ø     Create segment OB and highlight O, then choose “Circle by center+radius” under Construct

Ø     Highlight the circle, point B, and point C, then choose “Arc on circle” under Construct

2)    Construct a segment TB such that TB is tangent to the segment BOC at point B.

Ø     Highlight segment BC and the point B, then choose “Perpendicular line” under Construct

Ø     Highlight the new line and choose “Point on the perpendicular line” under Construct : label this point T

(You can drag this point along the perpendicular line)

3)    Construct segment AB on the end of BOC such that AB = BO

Ø     Highlight points B and O, then choose “Line” under Construct

Ø     Highlight segment BO and point B, then choose “Circle by center+radius” under Construct

Ø     Click on the intersection of line BO and the circle: label this point A

Ø     Highlight points A and B, then choose “Segment” under Construct

4)    Construct the end of the tomahawk

Ø     Highlight line TB, then choose “Point on perpendicular line” under Construct : label this point P

Ø     Highlight point P and point A, then choose “Segment” under Construct

Ø     Move point P so that angle BAP is about 28 degrees and point P lies on segment TB

Ø     Highlight point P and point T, then choose “Segment” under Construct

5)    Hide all lines and circles

Ø     Highlight all lines (not segments) and circles, then choose “Hide Path Objects” under Display

6)    Construct the handle of the Tomahawk

Ø     Highlight arc BC, then choose “Point on Arc” under Construct  : label this point R

Ø     Move point R so that it is closer to point B and the same distance as P away from segment AC

Ø     Highlight segment TP and point R, then choose “Parallel Line” under Construct

Ø     Highlight segment TP and point T, then choose “Perpendicular Line” under Construct

Ø     Click on the intersection of the parallel and perpendicular line :  label this point Q

Ø     Highlight points T and Q, then choose “Segment” under Construct

Ø     Highlight points Q and R, then choose “Segment” under Construct

Ø     Highlight the lines, then choose “Hide Objects” under Display

Ø     You can adjust the length of your handle by moving point T.

*An extension would be to construct a curved handle at the end of the handle and a curved segment AP.

     7)  Hide the semi-circle and create arc RC

Ø     Highlight segment BO and point O, then choose “Circle by center+radius” under Construct

Ø     Highlight the circle, point R and point C respectively, then choose “Arc on Circle” under Construct

Ø     Highlight arc BRC and the circle, then choose “Hide Objects” under Display

   * Another extension would be to construct grooves in your tomahawk at points B and O.

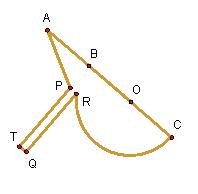
Congratulations, you have created your own tomahawk!

 

*Challenge:  Create the tomahawk for an angle starting with your angle.

 

The Tomahawk Trisector

 

 

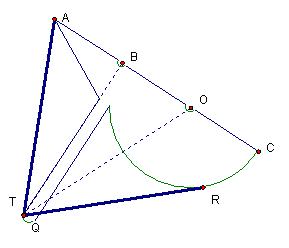
When given any angle, you can use the tomahawk that we just created to trisect an angle.

If you adjust the tomahawk such that one ray of the angle runs through point A and the other side of the angle is tangent to arc RC, the tomahawk trisects the given angle.  The three equivalent angles are angle ATB, angle BTO, and the angle formed by the ray through points T and O and the ray that passes through point T and O and the tangent point to arc RC.

 

Click here to manipulate the tomahawk and angle:  Trisector

 

Proof of why the the tomahawk works as an angle trisector:

 

For any given angle, we can adjust the tomahawk such that one ray runs through points T and A and the other ray runs through point T and is tangent to arc RC.

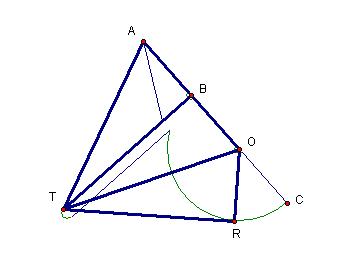
Since points B and R are tangent points to circle O through point T, angle TBO and angle TRO are right angles.  Angle TBA is also a right angle (*) since angle TBA is supplementary to angle TBO.  So, we have three right triangles. 

 

Since segments OB and OR are both radii of circle O, they are congruent.  By construction, OB = BA, so AB = BO = OR.  Thus, we have a side and angle that are congruent in each of the three triangles (TBA, TBO, TRO).

 

Since points B and R are tangent points to circle O through point T, we also know that TB = TR.  By the reflexive property, TB = TB.  Thus, TB = TB = TR.  Therefore, triangles TBA, TBO, and TRO are congruent by the Side Angle Side theorem. 

 

Angles BTA, BTO, and RTO are congruent because Corresponding parts of congruent triangles are congruent (CPCTC).  Therefore, the tomahawk is a tool for trisecting any given angle provided point A lies on a ray of the angle and point R lies on a ray and is tangent to circle O through point T. 

 

 

The Tomahawk as a Cube Root Tool

(Proof sketch found in Geometrical Tools:  A Mathematical Sketch & Model Book by Robert C. Yates)

 

 

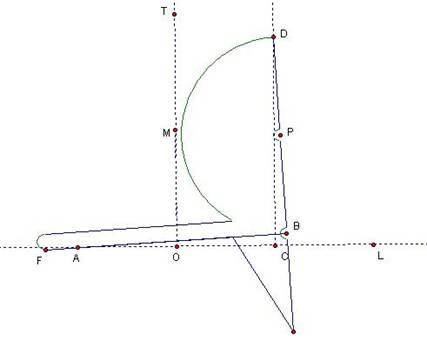
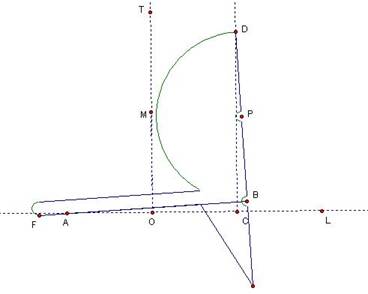
Cissoid of Diocles

Corner D moves along the fixed line CD while the outer edge BA passes through the fixed point A, located 2 units from CD.  The path of the midpoint, P, of BD is the cissoid. 

 

Proof that point P forms the Cissoid:

Let AC be the x-axis and its perpendicular bisector be the y-axis.   BD = AC = 2 by construction and AB = DC. 

Let P = (x,y),    B = (h,k),     D = (1,z).

Since P is the midpoint of BD,

x = (1+h)/2          y = (z+k)/2

2x = 1+h             2y = z+k

h = 2x-1             k = 2y-z

 

 

 

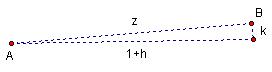
In all positions, AB = CD, so         (1+h)2 + k2 = z2

      Substituting for h and k:      (1+2x-1)2 + (2y-z)2 = z2

                                          4x2+4y2-4yz+z2=z2

                              X2+y2-yz = 0

                              X2+y2 = yz

                              z = (x2+y2)/y

 

Then, since AB is perpendicular to BD, their slopes are negative reciprocals.  So,

 

 

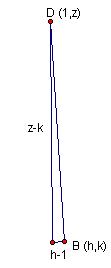
Slope of AB = k/(1+h)          Slope of BD    = (z-k)/-(h-1)

                                                      = (-1)(k-z)/(-1)(h-1)

                                                      = (k-z)/(h-1)

 

k/(1+h) = (-1)(h-1)/(k-z)

k/(1+h) = (1-h)/(k-z)

We can now substitute with equations from above for k, h, and z :

                        h = 2x-1             k = 2y-z              z = (x2+y2)/y

h+1 = 2x             k-z = 2y-z-z

1-h = 1-(2x-1)      k-z = 2(y-z)

1-h = 2-2x

1-h = 2(1-x)

 

k/(1+h) = (1-h)/(k-z)

(2y-z)/2x = 2(1-x)/2(y-z)

(2y-z)/2x = (1-x)/(y-z)

2x(1-x) = (2y-z)(y-z)

2x-2x2=2y2-3yz+z2

   Substituting for yz and z2 (from above) we get:

                        2x-2x2=2y2-3(x2+y2)+[(x2+y2)/y]2

2x-2x2-2y2=-3x2-3y2+[(x2+y2)/y]2

Y2+x2+2x=[(x2+y2)/y]2

    Multiply by y2:  y4+y2x2+2y2x = (x2+y2)2  

                        y4+y2x2+2y2x = x4+2x2y2+y4

                                      0=x4+x2y2-2y2x

    Divide by x:      0=x3+y2x-2y2

2y2-y2x=x3

Y2(2-x)=x3

Y2 = x3/(2-x)               This is the equation of the Cissoid of Diocles having

                              X=2 as Asymptote and cusp at (0,0).

 

Proof that the Tomahawk creates a cube root of a given length:

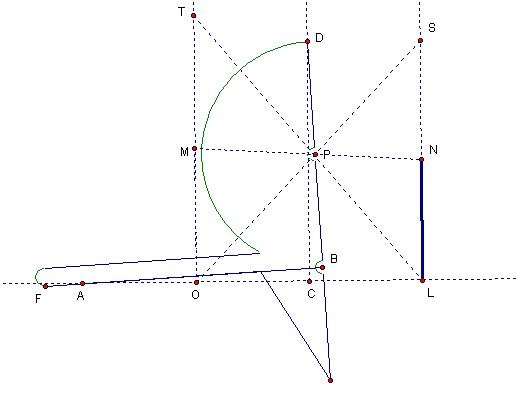
Let OL = 2 and its perpendicular OM=R, OT = 2R.  Then, Draw LT and move the tomahawk through point A (keeping point D on CD) until P lies on LT.  Draw MNP.  I will prove that LN = cube root of R.

Remember that P forms the Cissoid of Diocles (proof above) which has the equation Y2 = x3/(2-x).

Then,                       Y2 = x3/(2-x)

                              Y2(2-x)=x3

                              2y2-xy2=x3

      Multiplying by y:     2y3-xy3=x3y

                              Y3(2-x)=x3y

                              Y3/x3=y/(2-x)

                              (y/x)3=y/(2-x)

Now, a line OS runs through OP and has the equation,  y/x=m   , since P is the point (x,y).

So, substituting            m3=y/(2-x)

This equation may also be thought of as the line through (2,0) and P(x,y), which is the equation for the line LT.

 

The y-intercept is OT = 2m3 since T is the point of intersection.  Since LS = 2m and LN = LS/2, OM = OT/2, then

                                    (LN)3 = OM = R

 

So, LN is the cube root or R, or OM.  Thus, the tomahawk produces the cube root of any given length.

 

Cubic Root in GSP.

Return to Home Page