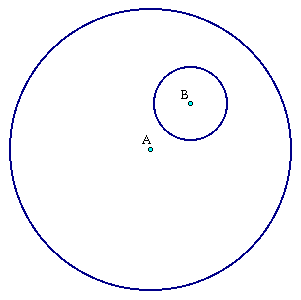
Given two circles A and B
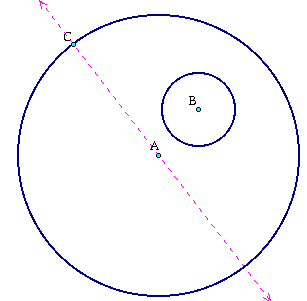
Pick a point on circle A, label it C and then draw a line through A and C.
Keeping in mind that the goal is to now have a circle that is tangent to circle B and line AC, we must now draw another circle with the same radius as circle B around circle C.
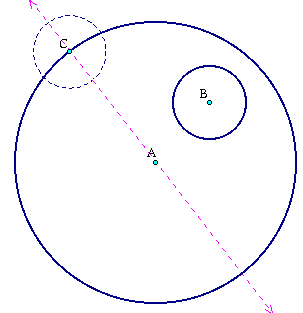
Next we must select the intersect of circle C with the line AC. This point is labeled D.
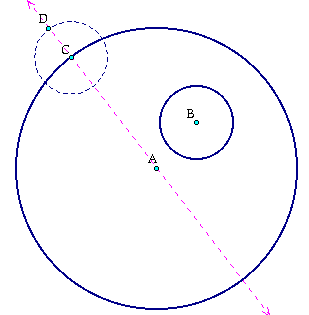
From the construction of C we know that circle C and circle B are the same and now we want to connect point D to point B, forming sement DB.

Now we want to find the midpoint (E) of line segment DB and then draw the perpindicular line from E.
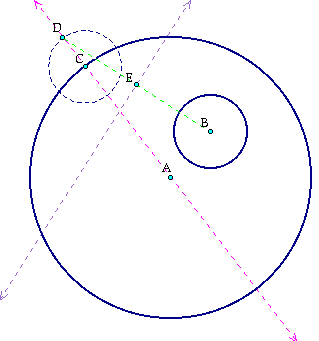
Next we want to make a point of the intersection (G) of the perpindicular line just drawn and the line AC. Then connect the segment GC.

This segment GC with the center at point G constructs the radius of our tangent circle to both circle B and circle A.
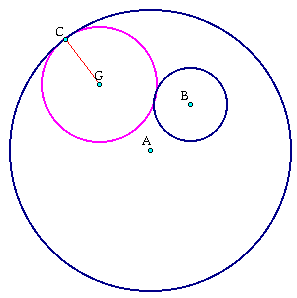
The final picture looks like this
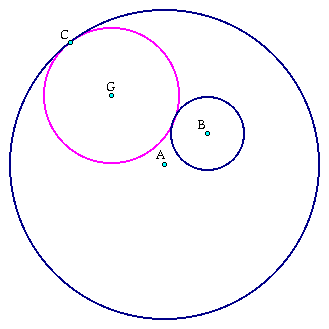
To play with the sketch click here (Must have GSP)
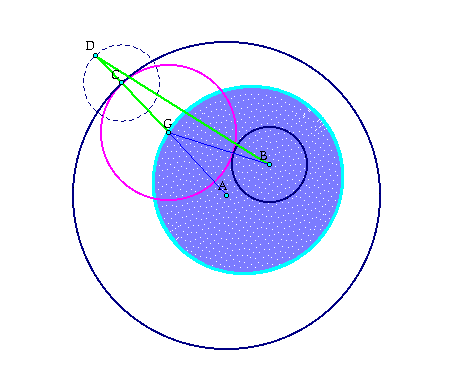
Now that this circle is drawn we can further examine by drawing a line connecting point B with point G. From this the line between AC can be unhidden and the intersection will be seen at point G. Additionally a line segment can be drawn from point B to point G.
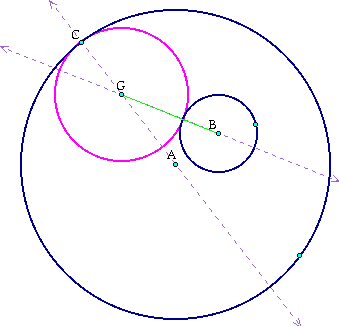
The line segment is always the length of the sum of the radius of circle B and the radius of circle G. When the extended circle is brought back into the picture, the presents of an isosceles triangle begins to appear.
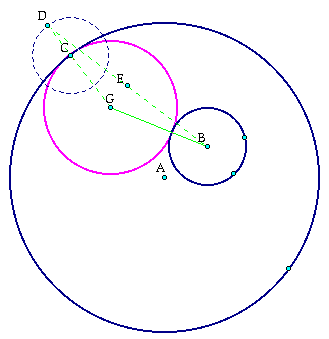
If GD are connected by a line segment, then we know that DG=BG because circle D was formed by the radius of circle B. If we connect point D with point B then we have formed a triangle DBG and the sides DG and BG are equal, therefore creating an isosceles triangle.
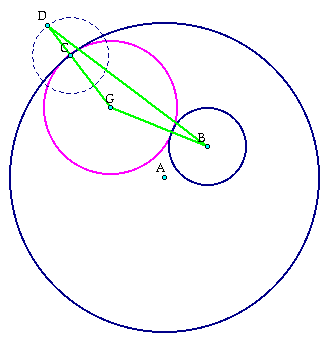
Now while this picture shows both the isosceles triangle formed as well as the circle tangent to both the large and small original circles, circle G is not the only circle that can be developed. In fact there are a large number that can be developed. This large number of points that satisfy the picture above, can be called loci. A locus is a representation for a set of points that can be the solution of a given problem. This can be seen best when we rotate point C along the circle A and look at the different circles represented for G. Click here to do that (GSP).
Now this movement of the circle can be seen even better through a visual representation of the loci. The locus of the circles appears as
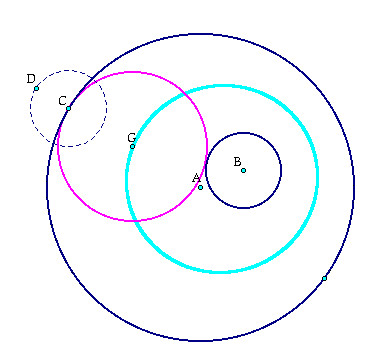
To see this in GSP and experiment, click here.
In essence the trace of segment GB will include all of the connections of segment GA and the trace will be all of the lines of the foci. rather than just the centers. The picture appears as: