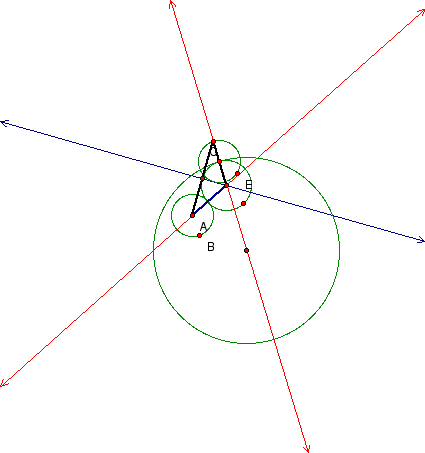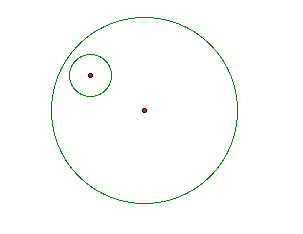
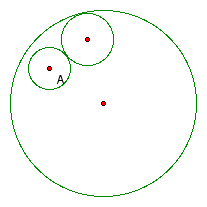
We begin by examining two arbitrary circles with one enclosed in the other and seek to find a circle

that is tangent to both.

Geometry sketch pad allows many approaches of solving the above problem for a variety level of students.

-Less experienced students may take a hit or miss approach taking advantage of an electronic

drawing program's forgiving features.

 

-Immediate or advanced students may take a logical or even an analytical approach to produce exact

results.

To play with sketchpad with the enclosed circle tool click here

The methods for producing the results asked for above may vary. Typically one wants to construct something like this.

 

With several attempts of creating perpendicular lines and creating congruent and similar triangles, one may get a result like this......

 

 

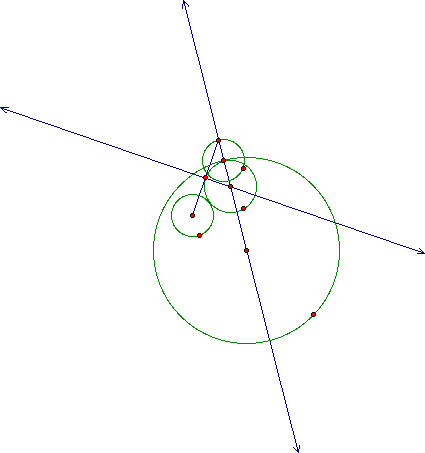
Notice below , the isosceles triangle formed from midpoints and radii of the circles in question. Notice also, that the created tangent circle with point E is divided

into 6 equal pieces by the three intersecting lines. Further finding relationships of this type (triangles, circles, and parallelsim) is a continuing challenging feat.

To explore with the above drawing click here

To explore a further examples of action traces choose below

 

 

Apple trace of two co-linear points

 

Trace of line trough center of the two tangent circles

Return