We consider a triangle ABC and an arbitrary point P, inside the triangle.

We draw lines from each vertex of the triangle through P, and observe as they intersect the

opposite sides of the triangle.

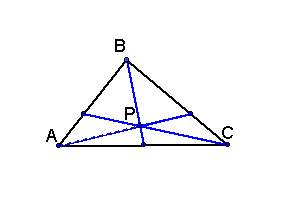
We see 6 to 13 new triangles formed from this new point. We want to look at some

relationships, so lets consider the sketch as a whole with the points of intersection of the

sides and lines from each vertex called F, D, E.

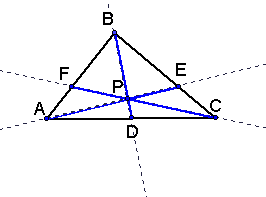
To play with the triangle above and see the measurements of various segment lengths as the angles change click here.

We want to pay particular attention to the relationships of the alternating segments that make up the large triangle ABC. Specicifically we want to examine

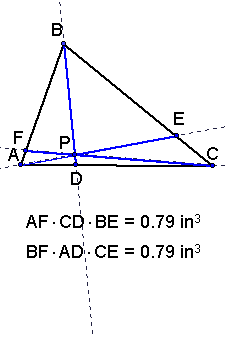
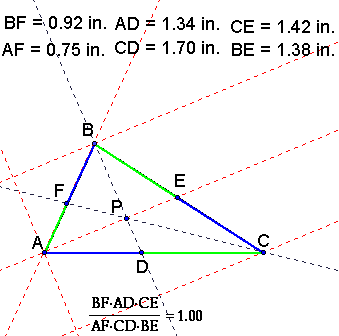
(BF)(AD)(CE) and (FA)(DC)(EB)

to see the values of the products with different choices of P, click here

You will find that as long as P, is inside the triangle, the products are equal. A sample triangle is pictured below.

To further prove this case we first consider that the ratio of

(BF)(AD)(CE) and (FA)(DC)(EB) =1

 

and

We speculate that shifting P augments respectivly each alternating segment of the larger triangle, but why is the product of the alternating sides always 1?

We try and look for some similar triangles with the creation of 2 new lines parallel to segment FP and discover the similar triangles below.

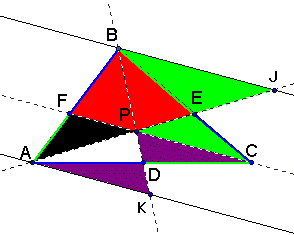We point out that

1. JBE ~ CPE

2.CDP~ ADK

3.AKB~ FPB

4. BJA~ FPA

Click here to explore the similar triangles

From the above ratio (BF)(AD)(CE) / (FA)(DC)(EB) =1, using a variety algebraic

steps and set ups we want to show

(BF)(AD)(CE) = (FA)(DC)(EB)

using the following ratios of similar triangles leads us to many methods to show the desired outcome.

(AD)=(AK)(CD)/(PC)

(BF)=(FP)(BA)/(AK)

(CE)=(BE)(PC)/(JB)

(CD)=(AD)(PC)/(AK)

(FA)=(FP)(BA)/(BJ)

(BE)=(CE)(JB)/(PC)

One particular dirction leads to

(FP)(BA)(AK)(CD)(BE)(PC)/(AK)(PC)(JB) =

(AD)(PC)(FP)(BA)(CE)(BJ) /(AK)(BJ)(PC). After some lengthy work by substitution,and multiplying by inverses you may arrive at several results which should be equivalent to the original conjecture.. that

(BF)(AD)(CE) - (FA)(DC)(EB) =0 =>

(BF)(AD)(CE) = (FA)(DC)(EB) and

(BF)(AD)(CE) / (FA)(DC)(EB) =1.

 

We want to last construct a new triangle using the points of intersection FDE that will have an interior point P.

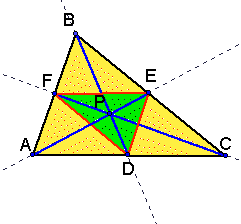
We want to look at the areas of triangle ABC and FED and compare. For different values of P...

Is there a minimum ratio?

Is there a maximum ration?

Where do these occur?

Click here to manipulate P, and see the areas of the triangles vary.

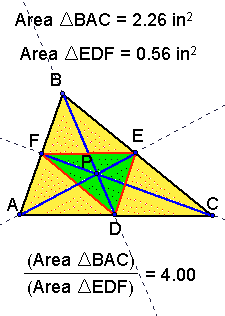
From this exercise we see that the ratio of the two triangles will always be greater than or equal to 4 when P is inside the triangle. The minimum ratio of 4 occurs when P is the orthocenter, and the maximum occurs (when EFD is the smallest as possible)...

The Minimum ratio (P is the orthocenter)

Tha Maximum ratio occurs when EDF is the degenerate triangle, and as the area approaches this limiting value the ratio approaches infinity.

 

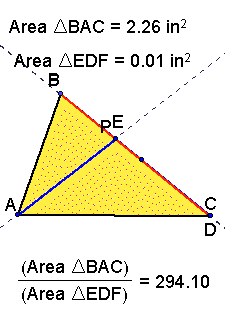
The above cases of area are only generalized for the case where P is on the triangle or inside the triangle. If P is outside the conjecture does not hold and the geometry then becomes more complex and outside the scope of this investigation.

Return