![]()
The Spreadsheet in Mathematics Explorations
By Donna Greenwood
![]()
The spreadsheet is a utility tool that can be adapted to many different explorations, presentations and simulations in mathematics. This write up explores the Fibonacci sequence using Excel.
Click here for the spreadsheet. Here’s the data for the Fibonacci sequence.
|
Fibonacci Numbers |
Ratio of terms |
Ratio of 2nd terms |
Ratio of 3rd terms |
Ratio of 4th terms |
Ratio of 5th terms |
|
1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|
3 |
1.5 |
3 |
3 |
|
|
|
5 |
1.666666667 |
2.5 |
5 |
5 |
|
|
8 |
1.6 |
2.66666667 |
4 |
8 |
8 |
|
13 |
1.625 |
2.6 |
4.33333333 |
6.5 |
13 |
|
21 |
1.615384615 |
2.625 |
4.2 |
7 |
10.5 |
|
34 |
1.619047619 |
2.61538462 |
4.25 |
6.8 |
11.3333333 |
|
55 |
1.617647059 |
2.61904762 |
4.23076923 |
6.875 |
11 |
|
89 |
1.618181818 |
2.61764706 |
4.23809524 |
6.84615385 |
11.125 |
|
144 |
1.617977528 |
2.61818182 |
4.23529412 |
6.85714286 |
11.0769231 |
|
233 |
1.618055556 |
2.61797753 |
4.23636364 |
6.85294118 |
11.0952381 |
|
377 |
1.618025751 |
2.61805556 |
4.23595506 |
6.85454545 |
11.0882353 |
|
610 |
1.618037135 |
2.61802575 |
4.23611111 |
6.85393258 |
11.0909091 |
|
987 |
1.618032787 |
2.61803714 |
4.2360515 |
6.85416667 |
11.0898876 |
|
1597 |
1.618034448 |
2.61803279 |
4.23607427 |
6.85407725 |
11.0902778 |
|
2584 |
1.618033813 |
2.61803445 |
4.23606557 |
6.85411141 |
11.0901288 |
|
4181 |
1.618034056 |
2.61803381 |
4.2360689 |
6.85409836 |
11.0901857 |
|
6765 |
1.618033963 |
2.61803406 |
4.23606763 |
6.85410334 |
11.0901639 |
|
10946 |
1.618033999 |
2.61803396 |
4.23606811 |
6.85410144 |
11.0901722 |
|
17711 |
1.618033985 |
2.618034 |
4.23606793 |
6.85410217 |
11.0901691 |
|
28657 |
1.61803399 |
2.61803399 |
4.236068 |
6.85410189 |
11.0901703 |
|
46368 |
1.618033988 |
2.61803399 |
4.23606797 |
6.854102 |
11.0901698 |
|
75025 |
1.618033989 |
2.61803399 |
4.23606798 |
6.85410196 |
11.09017 |
|
121393 |
1.618033989 |
2.61803399 |
4.23606798 |
6.85410197 |
11.0901699 |
|
196418 |
1.618033989 |
2.61803399 |
4.23606798 |
6.85410196 |
11.09017 |
|
317811 |
1.618033989 |
2.61803399 |
4.23606798 |
6.85410197 |
11.0901699 |
|
514229 |
1.618033989 |
2.61803399 |
4.23606798 |
6.85410197 |
11.0901699 |
With the spreadsheet, it’s really easy to set up the recursive formulas for the numbers and the ratios. It’s also a simple way to show just how quickly the ratios converge. The ratios of the first terms converge to the golden ratio (call it G). Here’s a graph that shows how quickly the terms converge to G:
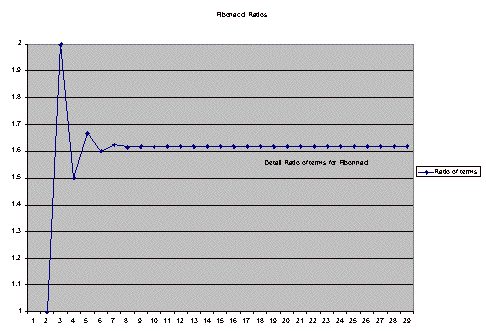
; the ratios of the second terms (i.e. every other term) converge to 1G + 1; the ratios of the third terms converge to 2G+1; the ratios of the fourth terms converge to 3G+1 and the ratios of the fifth to 4G+1.
Here’s a graph of all the ratios:

By graphing these together, you can see the similar shape of the graphs and how quickly each converges to its particular value.
Next, look at the Lucas sequence. This sequence starts with (2), 1 and 3 where the Fibonacci sequence starts with (0), 1 and 1.
|
Lucas Sequence |
Ratio of terms |
Ratio of 2nd terms |
Ratio of 3rd terms |
Ratio of 4th terms |
Ratio of 5th terms |
|
1 |
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
4 |
1.333333333 |
4 |
|
|
|
|
7 |
1.75 |
2.333333 |
7 |
|
|
|
11 |
1.571428571 |
2.75 |
3.666667 |
11 |
|
|
18 |
1.636363636 |
2.571429 |
4.5 |
6 |
18 |
|
29 |
1.611111111 |
2.636364 |
4.142857 |
7.25 |
9.666666667 |
|
47 |
1.620689655 |
2.611111 |
4.272727 |
6.714285714 |
11.75 |
|
76 |
1.617021277 |
2.62069 |
4.222222 |
6.909090909 |
10.85714286 |
|
123 |
1.618421053 |
2.617021 |
4.241379 |
6.833333333 |
11.18181818 |
|
199 |
1.617886179 |
2.618421 |
4.234043 |
6.862068966 |
11.05555556 |
|
322 |
1.618090452 |
2.617886 |
4.236842 |
6.85106383 |
11.10344828 |
|
521 |
1.618012422 |
2.61809 |
4.235772 |
6.855263158 |
11.08510638 |
|
843 |
1.618042226 |
2.618012 |
4.236181 |
6.853658537 |
11.09210526 |
|
1364 |
1.618030842 |
2.618042 |
4.236025 |
6.854271357 |
11.08943089 |
|
2207 |
1.618035191 |
2.618031 |
4.236084 |
6.854037267 |
11.09045226 |
|
3571 |
1.61803353 |
2.618035 |
4.236062 |
6.854126679 |
11.09006211 |
|
5778 |
1.618034164 |
2.618034 |
4.23607 |
6.854092527 |
11.09021113 |
|
9349 |
1.618033922 |
2.618034 |
4.236067 |
6.854105572 |
11.09015421 |
|
15127 |
1.618034014 |
2.618034 |
4.236068 |
6.854100589 |
11.09017595 |
|
24476 |
1.618033979 |
2.618034 |
4.236068 |
6.854102492 |
11.09016765 |
|
39603 |
1.618033992 |
2.618034 |
4.236068 |
6.854101765 |
11.09017082 |
|
64079 |
1.618033987 |
2.618034 |
4.236068 |
6.854102043 |
11.09016961 |
|
103682 |
1.618033989 |
2.618034 |
4.236068 |
6.854101937 |
11.09017007 |
|
167761 |
1.618033989 |
2.618034 |
4.236068 |
6.854101977 |
11.09016989 |
|
271443 |
1.618033989 |
2.618034 |
4.236068 |
6.854101962 |
11.09016996 |
|
439204 |
1.618033989 |
2.618034 |
4.236068 |
6.854101968 |
11.09016994 |
|
710647 |
1.618033989 |
2.618034 |
4.236068 |
6.854101966 |
11.09016995 |
|
1149851 |
1.618033989 |
2.618034 |
4.236068 |
6.854101966 |
11.09016994 |
This convergence of the ratios is the same as the Fibonacci sequence.
Finally, here’s a random sequence beginning with -1 and -7:…
|
Random Sequence |
Ratio of terms |
Ratio of 2nd terms |
Ratio of 3rd terms |
Ratio of 4th terms |
Ratio of 5th terms |
|
-1 |
|
|
|
|
|
|
-7 |
7 |
|
|
|
|
|
-8 |
1.142857143 |
8 |
|
|
|
|
-15 |
1.875 |
2.142857 |
15 |
|
|
|
-23 |
1.533333333 |
2.875 |
3.285714 |
23 |
|
|
-38 |
1.652173913 |
2.533333 |
4.75 |
5.428571 |
38 |
|
-61 |
1.605263158 |
2.652174 |
4.066667 |
7.625 |
8.714286 |
|
-99 |
1.62295082 |
2.605263 |
4.304348 |
6.6 |
12.375 |
|
-160 |
1.616161616 |
2.622951 |
4.210526 |
6.956522 |
10.66667 |
|
-259 |
1.61875 |
2.616162 |
4.245902 |
6.815789 |
11.26087 |
|
-419 |
1.617760618 |
2.61875 |
4.232323 |
6.868852 |
11.02632 |
|
-678 |
1.618138425 |
2.617761 |
4.2375 |
6.848485 |
11.11475 |
|
-1097 |
1.6179941 |
2.618138 |
4.235521 |
6.85625 |
11.08081 |
|
-1775 |
1.618049225 |
2.617994 |
4.236277 |
6.853282 |
11.09375 |
|
-2872 |
1.618028169 |
2.618049 |
4.235988 |
6.854415 |
11.0888 |
|
-4647 |
1.618036212 |
2.618028 |
4.236098 |
6.853982 |
11.09069 |
|
-7519 |
1.61803314 |
2.618036 |
4.236056 |
6.854148 |
11.08997 |
|
-12166 |
1.618034313 |
2.618033 |
4.236072 |
6.854085 |
11.09025 |
|
-19685 |
1.618033865 |
2.618034 |
4.236066 |
6.854109 |
11.09014 |
|
-31851 |
1.618034036 |
2.618034 |
4.236069 |
6.854099 |
11.09018 |
|
-51536 |
1.618033971 |
2.618034 |
4.236068 |
6.854103 |
11.09017 |
|
-83387 |
1.618033996 |
2.618034 |
4.236068 |
6.854102 |
11.09017 |
|
-134923 |
1.618033986 |
2.618034 |
4.236068 |
6.854102 |
11.09017 |
|
-218310 |
1.61803399 |
2.618034 |
4.236068 |
6.854102 |
11.09017 |
|
-353233 |
1.618033988 |
2.618034 |
4.236068 |
6.854102 |
11.09017 |
|
-571543 |
1.618033989 |
2.618034 |
4.236068 |
6.854102 |
11.09017 |
|
-924776 |
1.618033989 |
2.618034 |
4.236068 |
6.854102 |
11.09017 |
|
-1496319 |
1.618033989 |
2.618034 |
4.236068 |
6.854102 |
11.09017 |
|
-2421095 |
1.618033989 |
2.618034 |
4.236068 |
6.854102 |
11.09017 |
Here’s a comparison of the convergence of the first terms of the three sequences listed here:

After the initial jumping around to account for the differences in the first terms, the terms converge rapidly – by about the 6th number in the sequence there’s no measurable difference in the ratios, at least as far as the graph is concerned.
Last but not least, I wanted to compare the recursive formula – an = an-1 + an – to the closed form of the equation, which is
an = 1/sqrt(5) * (((1 + sqrt(5))/2)n – ((1 - sqrt(5))/2)n). I expected to see some round off error based on the way the spreadsheet would handle the square roots raised to a power. Here are the results:
|
Fibonacci Numbers |
Closed Formula |
|
1 |
1 |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
5 |
5 |
|
8 |
8 |
|
13 |
13 |
|
21 |
21 |
|
34 |
34 |
|
55 |
55 |
|
89 |
89 |
|
144 |
144 |
|
233 |
233 |
|
377 |
377 |
|
610 |
610 |
|
987 |
987 |
|
1597 |
1597 |
|
2584 |
2584 |
|
4181 |
4181 |
|
6765 |
6765 |
|
10946 |
10946 |
|
17711 |
17711 |
|
28657 |
28657 |
|
46368 |
46368 |
|
75025 |
75025 |
|
121393 |
121393 |
|
196418 |
196418 |
|
317811 |
317811 |
|
514229 |
514229 |
As you can see, there’s not a bit of error! That was a nice surprise, especially since this was the formula I had to key into the spreadsheet:
=1/SQRT(5)*(POWER((1+SQRT(5))/2,B2) - POWER((1-SQRT(5))/ 2, B2))
Note: B2 is a hidden value that represents n in the prior equation.
