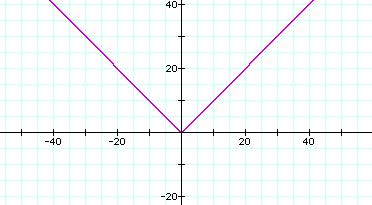
Here again, we will use f(x) = |x| as our parent function.
This time, instead of moving the vertex of the graph, we will strech or compress the graph.
It might be simpler to think of a stretch or a compression in terms of a rubber band. When in its original state, it has a certain interior. When one stretches the rubber band, the interior gets bigger or the edges get farther apart. When one compresses the rubber band, the interior gets skinnier or the edges get closer together. The same thing happens to our graph.
So, look at the graph below. It has the parent function in purple, a vertical strech in red, and a vertical compression in blue.
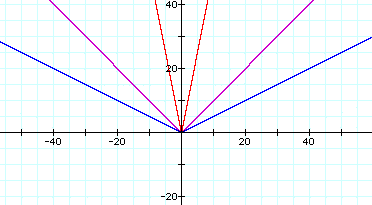
Notice that the horizontal compression has moved the sides closer together or made the interior angle smaller while thehorizonal stretch has moved the sides farther apart or made the interior angle larger.
The equations used to make the strech and compression are:
and
. Which
equation do you think goes with which graph?
If you guessed that the red graph is
and the blue graph is 
then
you are correct.
Now, based on this can you make generalizations about horizontal stretches and compressions? If you would like a little more help, click here to see a movie of the parent function going through horizontal stretches and compressions.
The Rule for Horizontal Stretches and Compressions:
if y = f(x), then y = f(bx) gives a horizontal stretch when 0 < b < 1 and a horizontal compression when b > 1.
Note that unlike translations where there could be a more than one happening at any given time, there can be either a horizontal stretch or a vertical compression but not both at the same time.
Bonus: Did you notice a relationship between horizonatal and vertical compressions. 10 points for any one that can write up and throughly explain the relationship.