Parabolas have the general form:
Here, the a, h, and k transform the graph. Like the circle, the h and k affect the vertex of the parabola where with the circle it affected the center. The a will stretch or compress the graph.
Let's start with the h. The h is a horizontal translation of the vertex. Just like the circle, it is counter-intuitive due to the minus sign n the formula. Thus, a positive moves it left and a negative moves it right. For exapmple:
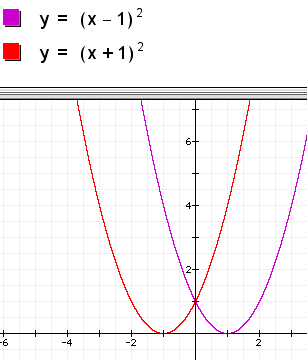
So, one can see the transformations moveed the parabolas left or right.
Next, consider the k. Unlike the k used in the circle, this transformation is intuitive. This is due to the addition sign in front of the k. This is a horizonatal translation of the vertex where a positve moves the vertex upward and the a negative moves the vertex downward. For example:
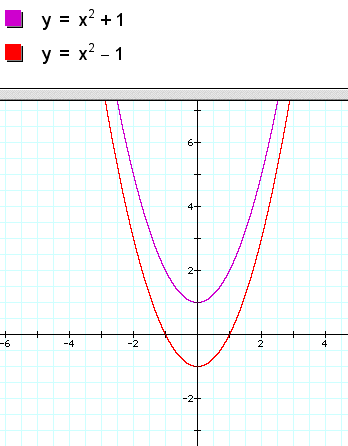
So, one can see the translations that occur when k is introduced into the function.
The a has three possiblities: stretch, compress, or reflect. The a stretches the graph when it is greater than 1. It compresses the graph when it is between 0 and 1, and it reflects the graph across the x-axis when it is negative.
An example of a strectch would be:
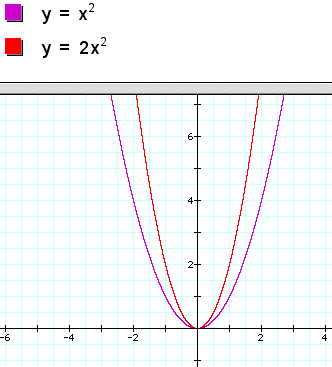
The purple parabola is the basic parabola and the red is the stretched parabola. Notice that it is skinnier than the parent graph or that the distance between the sides of the graph is smaller.
A compression works the same way, except that it gets wider instead of skinnier or the distance between the sides increases. For example:
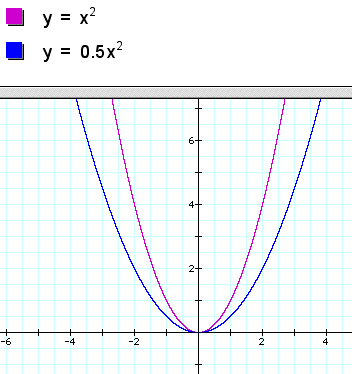
Here again, the purple is the parent function and the blue is the compressed function.
Finally, when the a is negative, the graph is reflected across the x-axis. So, instead of pointing upwards, it points downwards. Like so:
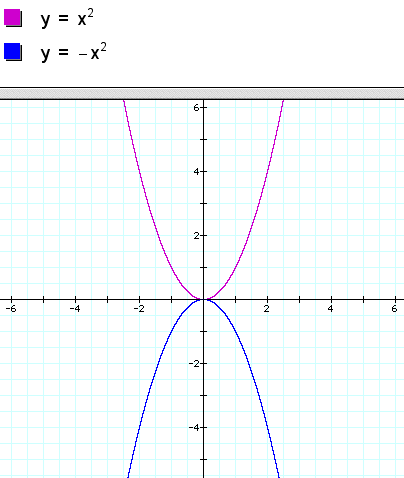
10-Point Bonus: What do you think happens to the translations of the following function: