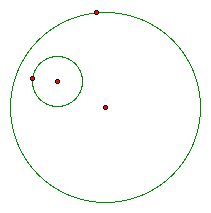
Given
two circles, one with a designated point on the outside, how can
we construct a third circle that is tangent to both?
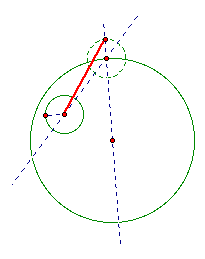
The construction involves creating a line through the center of the circle to the desired point of tangency on the outside. We then create a circle with the radius of the smaller circle that has as its center point the desired point of tangency.
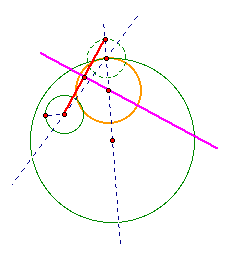We
can use the center of the original inside circle and the top intersection
of the new circle with the line through the center of the larger
circle to create a segment. The perpindicular bisector of this
segment will intersect with the original line through the center
of the circle at the center of the desired tangent circle.
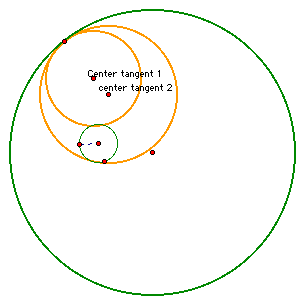
It is actually possible to create two circles that are tangent to the orginal circles.
We can see that the center of both circles are inside the
original circle with the desired point of tangency and that the centers are collinear with the center of the circle with the designated tangency point.
If the two circles intersect, where can we find the centers of the desired tangent circles?
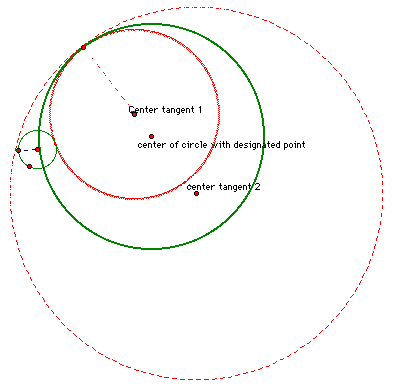Again
they are collinear with the center of the circle that contains
the desired tangency point.
What if the second circle lies entirely outside of the circle with the designated tangency point? We see that the centers of the tangent circles are not collinear with the center of the circle with the desired point of tangency:
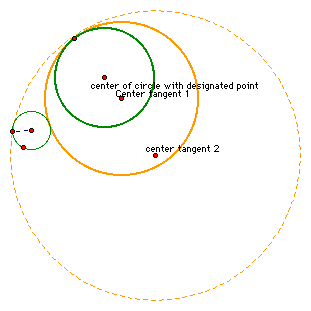Why is it that the
centers are collinear in every case except for the case in which
the smaller circle is completely external to the circle with the
desired point of tangency? Because in the final case the radial
measure for the larger tangent circle is equal almost to the diameter
of the smaller tangent circle and it is almost twice the diameter
of the circle with the desired tangency point. This difference
in measure, while requiring still that these 3 circles meet at
the same designated tangency point, requires that their centers
are no longer collinear.