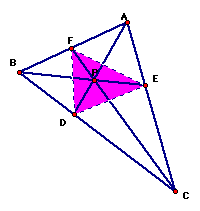
The focus of this assignment will be the triangle ABC, the randomly-selected point P, and the segments created from the lines drawn through the vertices and connecting the vertices to P.
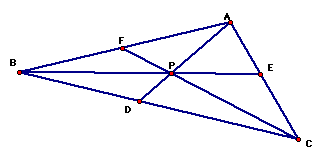
When we examine these segments for various shapes of triangles and locations of P, what can we conjecture about (AF)(BD)(EC) and (FB)(DC)(EA)?
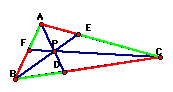
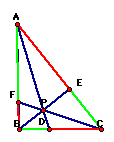
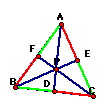
Conjecture: the ratio of (AF)(BD)(EC)/(FB)(DC)(EA) = 1 or ((AF)/(FB)) * ((BD)/(DC)) * ((EC)/(EA)) = 1
How can we prove this?
We can use Ceva's Theorem. Ceva's Theorem states that if (and only if) the product of the ratios of the side segments equals one, then the three cevians of the triangle are concurrent. The cevians of a triangle are the segments that join a vertex to a point on the opposite side of the triangle.
From Ceva's Theorem, we know that if the segments AD, BE and FC are concurrent (if they intersect at a point, which these segments do at point P), then the product of the ratios given above does equal one.
How can we show that Ceva's Theorem is true?
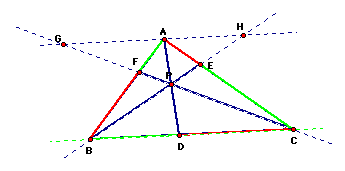When we extend the
segments FC and EB into lines, then create a line through point
A that is parallel to the segment BC, we can create triangles
that we know are similar. From the above diagram, we know that
AFG ~ BFC. Because they are similar, we know that AFG/BFC is equal
to AF/BF.
Since this can also be extended to triangles AEH and ECB in relation to segments AE/EC as well as the ratio of triangles ABD and ADC and the ratio of BD/DC.
Since we know that AFG/BFC = AF/BF, AEH/ECB = AE/EC, ABD/ADC = BD/DC, and we also know that (AFG/BFC)(AEH/ECB)(ABD/ADC)=1 (because the triangles are similar), then we know that (AF/BF)*(AE/EC)*(BD/DC)=1.
This proves the original conjecture.
If use lines instead of segments to construct the triangle ABC and locate point P outside of the triangle, then we have a construction that is a quadrangle. Click here for a GSP sketch of the triangle ABC and the point P that can be moved to outside of the triangle.
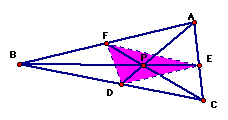
Looking at the following illustration, what could be conjectured about the areas of the triangles ABC and DEF? It has been propsed that ABC/DEF is always greater than 4, and it is equal to 4 under a special circumstance.
To show that ABC/DEF is greater than 4, we need to show that at least one of the triangles AFE, ECD and FBD has an area greater than the area of DEF. If they are equal to DEF, then the ratio of ABC/DEF will equal 4. The area of the triangles AFE, ECD and FBD are equal to the area of FDE when the vertices of FDE are located at the midpoints of the segments AC, BC and BA. This is illustrated below and can be proven to be true because the area of a triangle is calculated from its base and its altitude. In the case where DEF is formed from the midpoints of ABC, its altitude is the perpindicular line from its vertex F to the base point on DE. Because DE marks the midpoint of the triangle, we know that the segment from F to its altitude base is equal to the segment from C to its altitude base. Additionally, because F,D,E are midpoints, we know that the base DE is equal to the bases formed by EF,FD. Therefore, the areas must be equal and the ratio ABC/DEF is equal to 4(DEF)/DEF = 4.
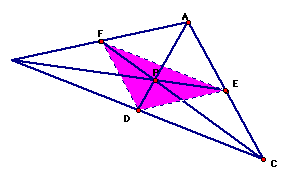
When the triangles do not have an area equal to DEF, then how can we know they have a greater area?
Following are two good starts to proofs but both hit a snag at the point where I was supposed to supply the information that we are trying to prove.... In sum I will conjecture that since we know the ratio is 4 when P is at the centroid and ABC is equilateral, any shift into a direction away from the centroid will reduce the size of the center triangle. When P=centroid, the interior triangle is at its maximum area.
Failed Proof Idea #1:
If we look at the
image to the left, we see that the ratio ABC/DEF is equal to the
ratio (DEF+AFE+BFD+CDE)/DEF. Since the area of triangle ABC can
be written as
Area ABC = sqrt(s(s-ac)(s-bc)(s-ab)) where s=perimeter/2, we can use what we know about all of the triangles's sides to compare them:
Area FBC= sqrt(s(s-fb)(s-bd)(s-fd))
Area FAE=sqrt(s(s-fa)(s-ae)(s-ef))
Area ECD=sqrt(s(s-ed)(s-dc)(s-ec))
Area EFD=sqrt(s(s-fd)(s-ed)(s-fe))
We can compare the area of EFD to each triangle individually to see if EFD is larger in area than any other triangle, since we have already determined that if they are equal the ratio=4 and we want to see why it is otherwise larger than 4.
Area EFD=sqrt(s(s-fd)(s-ed)(s-fe))< Area ECD=sqrt(s(s-ed)(s-dc)(s-ec)) if
(s(s-fd)(s-ed)(s-fe))<(s(s-ed)(s-dc)(s-ec))
We can factor out s and (s-ed) from boths sides.
(s-fd)(s-fe)<(s-dc)(s-ec)
Since s=perimeter/2, we can substitute
(ed+fd+ef-2fd)(ed+fd+ef-2fe)< (ed+ec+dc-2dc)(ed+ec+dc-2ec)
Failed Proof Idea #2:
Or we can use the standard calculation of area=.5(b)(h) where b=the length of the base segment and h=the length of the altitude, then we can rewrite this as:
((.5)(DE)(hFED)+(.5)(FE)(hFAE)+(.5)(ED)(hCED)+(.5)(FD)(hFBD))/((.5)(DE)(hFED)) and we can factor out .5 so that the ratio becomes:
((DE)(hFED)+(FE)(hFAE)+(ED)(hCED)+(FD)(hFBD))/((DE)(hFED))