Problem: A
Tangled Tale (click here to see the problem statement)
My solution.
Faux Pas:
I have to admit, I fell to the temptation to take the average
of the given rates and multiply the result by 5 hours.
Once I got my head screwed on straight(er), here's what I did:
Recognizing that RATE is the RATIO between
DISTANCE and TIME;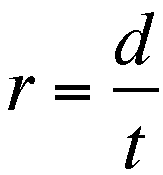
and that TIME can be determined by the
ratio; 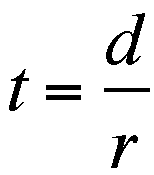 and that the TOTAL
TIME is
and that the TOTAL
TIME is 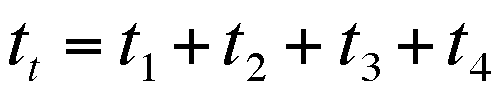 ;
;
I constructed the spreadsheet below.
Here I set up t-values for each leg of the trip, based on the
given rates for each leg, and looked for sums that equaled 5 (hours).
Note that the Distance for the fourth leg equals that of the first
(Level Ground), and that the distances of the second and third
legs (Uphill and Downhill) are equal. I started with the assumption
that each leg had a distance of 1 mile, then adjusted the Uphill
and Dowhnhill distances:
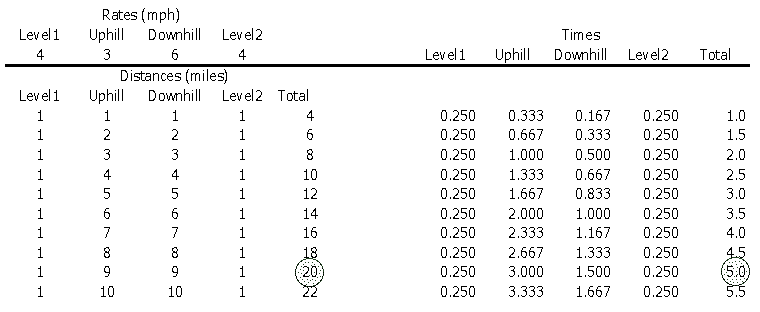
So with a Level Distance
of 1 mile and an Uphill/Downhill Distance of 9 miles, given the
rates of travel during each leg, resulted in a walk of 20 miles
over 5 hours.
I then fixed the Level Distance
at 2 miles and adjusted the Uphill/Downhill Distance. In this
case, 2 miles on level ground and 8 miles Uphill and Downhill
resulted in a 20 mile journey over 5 hours.
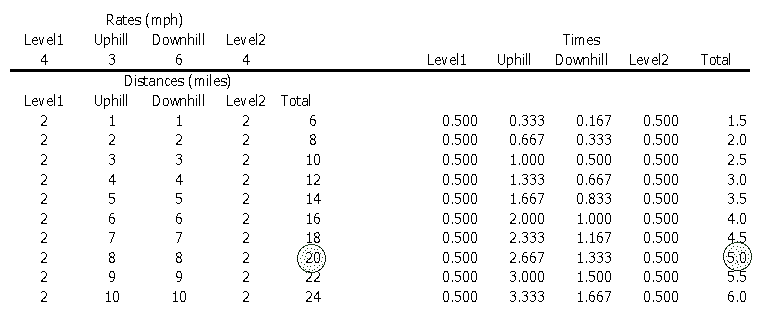
It seems that the total of
the Level Ground mileage and the Uphill/Downhill mileage is always
10, and therefore, the total Distance is always 20 miles:
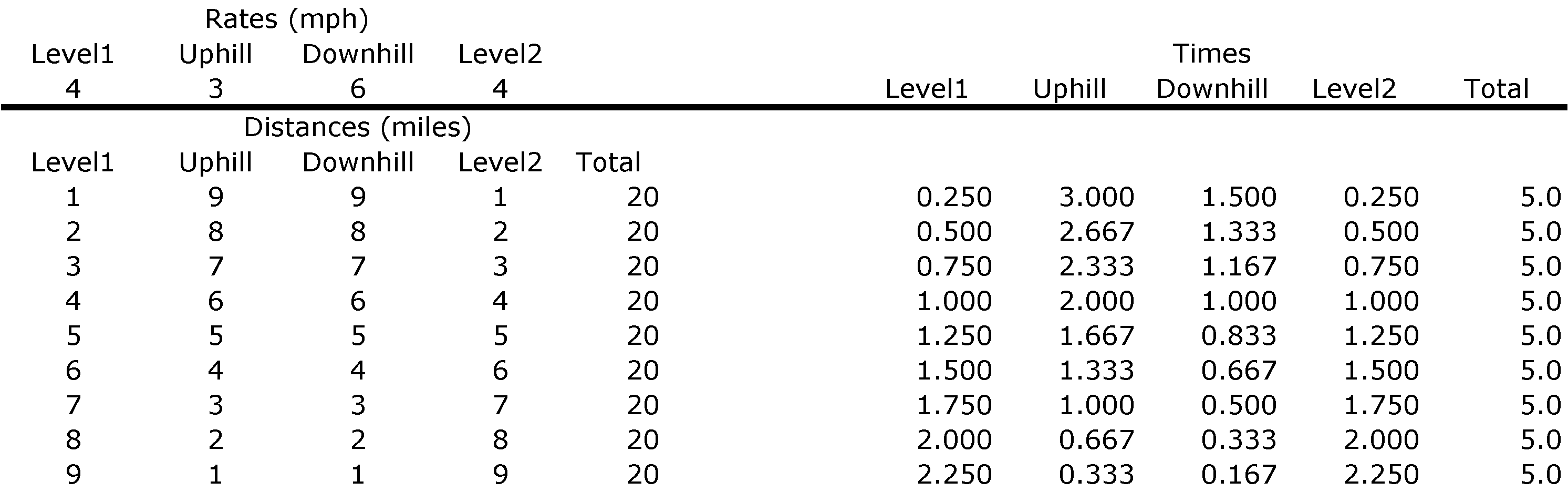
Examining the problem Algebraically.
As observed earlier, we are dealing with
RATE, DISTANCE, and TIME,
where RATE is expressed by; 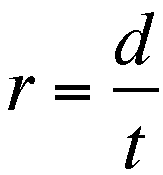
DISTANCE is expressed by; 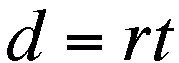
and TIME is expressed by; 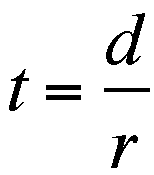 .
.
I designated the overall RATE as 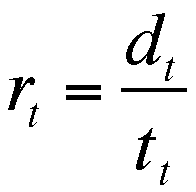
and the overall rate is also expressed
by; 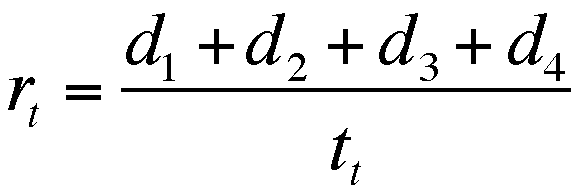 .
.
But as the Level Distance remained constant
on the first and fourth legs, then 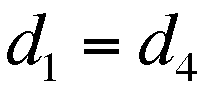 .
.
And the Uphill nd Downhill distances
were equal, so 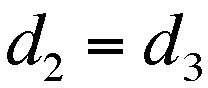 .
.
Therefore, the overall rate is simplified
to
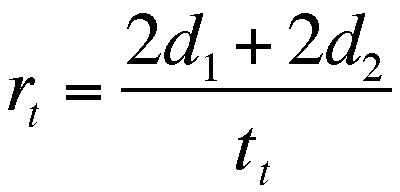
and reduced to
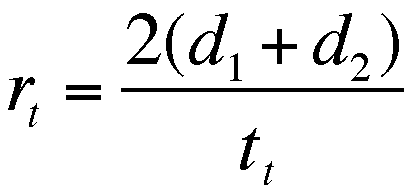 or
or 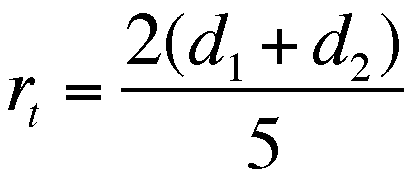 ,
,
as the total TIME was given to be 5 hours.
aaa
The Total TIME is
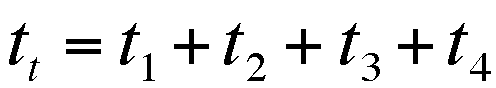
or
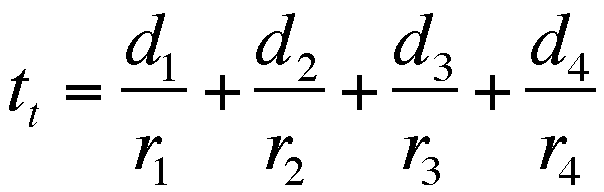 ,
,
and given values for the TOTAL TIME and
the RATE for each leg, we now have
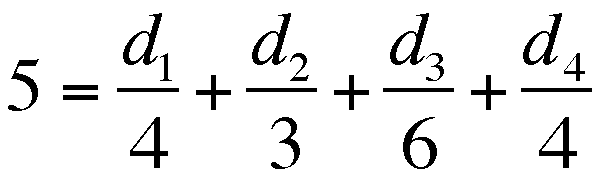 .
.
But again, as 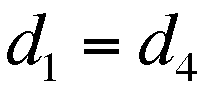 and
and 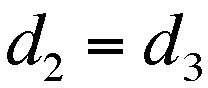 , then
, then
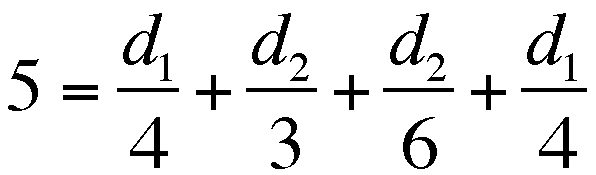
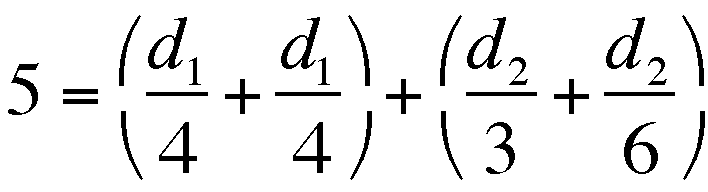
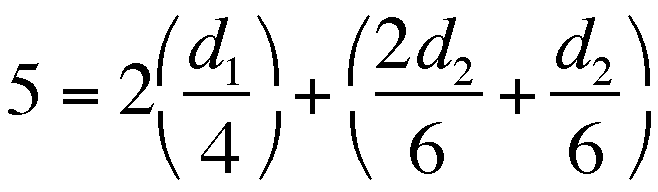
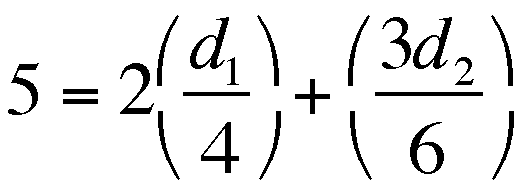
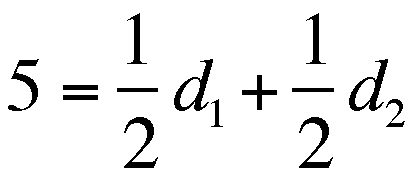
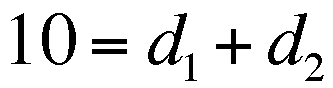 .
.
So the Total Distance is 20 miles.
The overal RATE, though not asked for
in the problem - I've gone this far, might as well keep going
- is 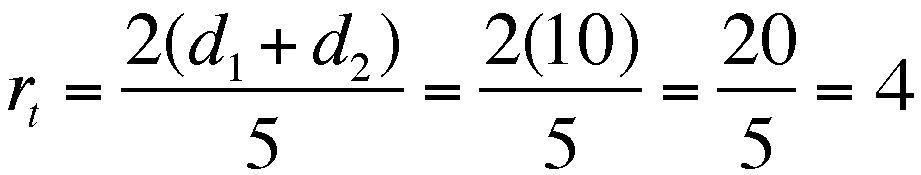 , 4 mph, that is.
, 4 mph, that is.
a a a
PS: I leave for the reader to consider
the meaning of the given situation if either the Level Distances
or Uphill/Downhill Distance are ZERO.
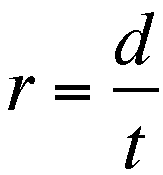
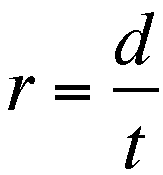
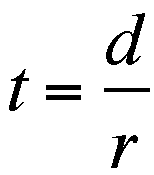 and that the TOTAL
TIME is
and that the TOTAL
TIME is 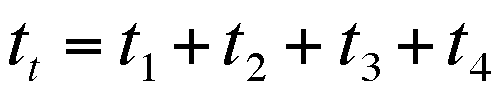 ;
;


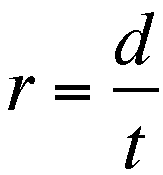
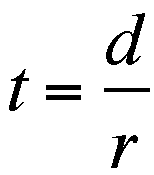 .
.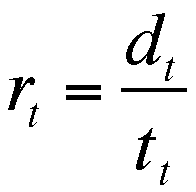
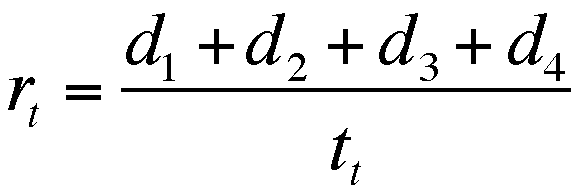 .
.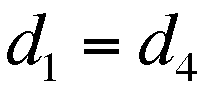 .
.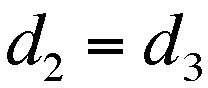 .
.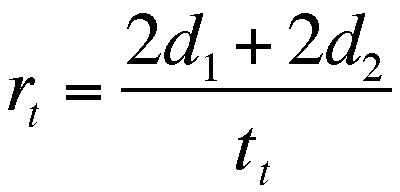
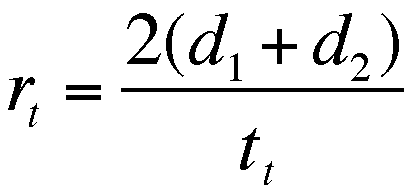 or
or 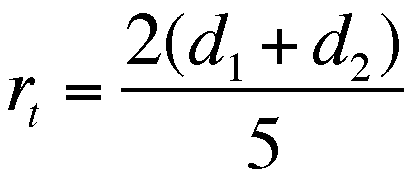 ,
,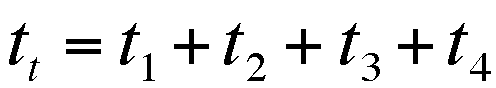
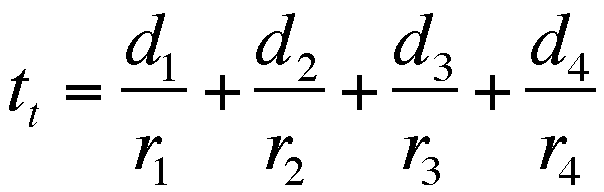 ,
,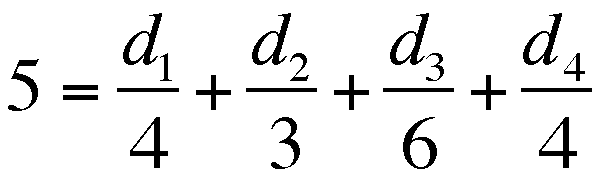 .
.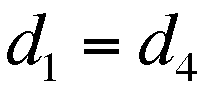 and
and 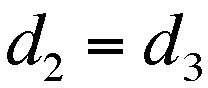 , then
, then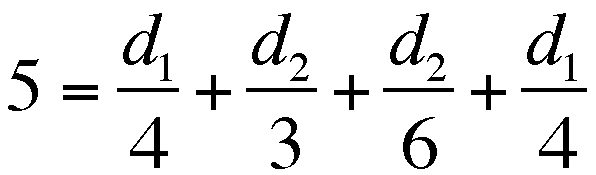
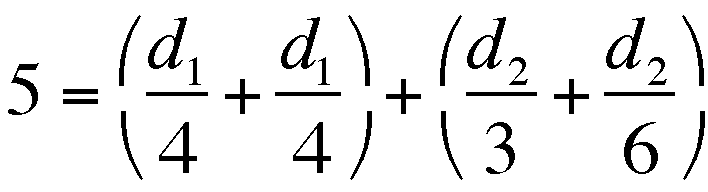
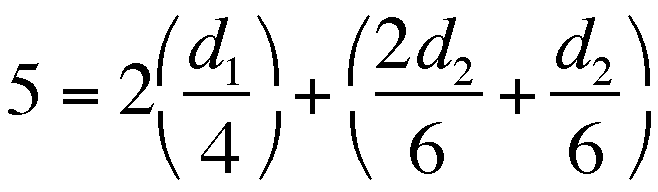
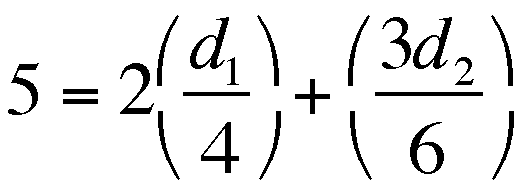
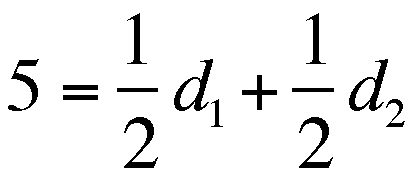
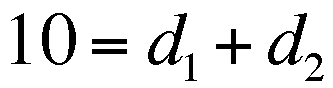 .
.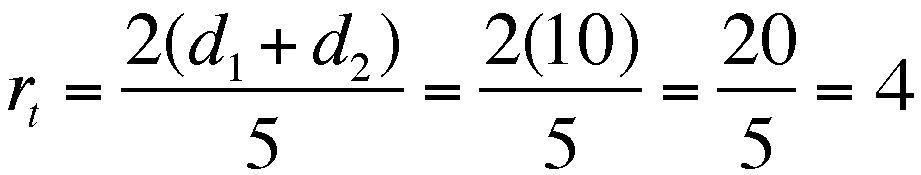 , 4 mph, that is.
, 4 mph, that is.