and 
(
is real number)In order to the observation, we notice the graph is always
the central symmetry with the center point of the origin. We can
observe or proof this feature according to search the intersections
of 
and 
. By this observation, we also
notice these equations haven't three intersections always. Through
algebraic approach of the equation, proof the feature of the central
symmetry and search the intersections of the equations.
Substance for
Then
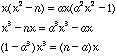
When 
the equation is conclusion with 
.Therefore,
if 
is any number, there is the intersection of the
origin.
When 
then
When 
because its discriminant is 
so 
Substance for 
then 
Therefore, when and, intersections
of the equations accord with
.
When and
,it
is not true, then there is only intersection of the origin.
When 
that is to say 
Then
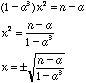
and
So, when , the coordinates of the intersection of the equations
without the origin are below.
Only the signs differ from coordinates of two intersections , so these two points are the central symmetry with the central point of the origin.
For these coordinate numbers are the real numbers :
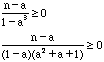
So 
and 
Or 
and 
Because of 
and
For 
and 
,when 
then
,when 
then 
For 
and 
,when then
,when then
Therefore, when , or
and when , or
As 
, then 
So when , the intersection is the only (0,0)
Conclusion
As and or 
,or
as 
and 
or , then
there are three intersections of
.
The first two points differ from only signs . It means central symmetry with center point of the origin.
As and 
, or as and
, then there is an only intersection of the origin.