and 
(a
is real number)Substance y = ax for
Then
When x=0 the equations is conclusion with y=0. Therefore, if a is any number, there is the intersection of origin.
When x not = 0 then 
If 
therefore a=1
Then ,substance a=1 for
Then 0=3
It's not true. Therefore, as a=1, there is only intersection of origin.
If a not =1
And
The coordinates of the intersections without the origin are below.
The only sings differ from the two coordinates, so these two points are the central symmetry with the central point of origin.
For these coordination numbers are the real number:
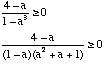
By the way
Therefore
For
and 
so 
or
and 
so 
Summary
As 
, there is the only intersection
of the origin.
As or ,there
are three intersections.
The intersections are
The two intersections of the first are the central symmetry with the center point of (0,0).